题目内容
8.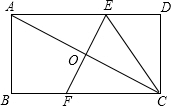 如图,在矩形ABCD中,AB=2,BC=4,将矩形沿EF折叠,使点A与点C重合,连接CE,则CE长为( )
如图,在矩形ABCD中,AB=2,BC=4,将矩形沿EF折叠,使点A与点C重合,连接CE,则CE长为( )| A. | 3.5 | B. | 3 | C. | 2.8 | D. | 2.5 |
分析 设BF=x,表示出CF=4-x,根据翻折的性质可得AF=CF,AE=CE,然后在Rt△ABF中,利用勾股定理列出方程求出x,再根据翻折的性质可得∠AFE=∠CFE,根据两直线平行,内错角相等可得∠AEF=∠CFE,然后求出∠AEF=∠AFE,根据等角对等边可得AE=AF,得出CE=AF=CF.
解答 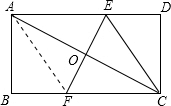 解:设BF=x,则CF=BC-BF=4-x,
解:设BF=x,则CF=BC-BF=4-x,
∵沿EF翻折后点C与点A重合,
∴AF=CF=4-x,AE=CE,
在Rt△ABF中,AB2+BF2=AF2,
即22+x2=(4-x)2,
解得x=$\frac{3}{2}$,
∴AF=CF=4-$\frac{3}{2}$=$\frac{5}{2}$,
由翻折的性质得,∠AFE=∠CFE,
∵矩形ABCD的对边AD∥BC,
∴∠AEF=∠EFC,
∴∠AEF=∠AFE,
∴AE=AF=$\frac{5}{2}$,
∴CE=AE=$\frac{5}{2}$.
故选D.
点评 本题考查了翻折变换的性质,矩形的判定与性质,勾股定理,熟记各性质并作利用勾股定理列方程求出BF的长度是解题的关键,也是本题的突破口.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
19.水是生命之源,水是由氢原子和氧原子组成的,其中氢原子的直径为0.0000000001m,把0.0000000001用科学记数法表示为( )
| A. | 1×109 | B. | 1×1010 | C. | 1×10-9 | D. | 1×10-10 |
 【知识迁移】
【知识迁移】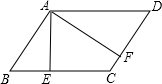 如图,在?ABCD中,AE⊥BC于点E,AF⊥CD于点F,若AE=4,AF=6,且?ABCD的周长为40,则?ABCD的面积为( )
如图,在?ABCD中,AE⊥BC于点E,AF⊥CD于点F,若AE=4,AF=6,且?ABCD的周长为40,则?ABCD的面积为( ) 如图,已知EF∥BD,∠1=∠2,∠C=48°,求∠ABC.
如图,已知EF∥BD,∠1=∠2,∠C=48°,求∠ABC.