题目内容
19.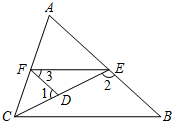 如图,已知∠1,∠2互为补角,且∠3=∠B,求证:∠AFE=∠ACB.
如图,已知∠1,∠2互为补角,且∠3=∠B,求证:∠AFE=∠ACB.证明:∵∠1+∠FDE=180°,∠l+∠2=180°
∴∠FDE=∠2
∴DF∥AB
∴∠3=∠AEF
又∵∠3=∠B
∴∠B=∠AEF
∴EF∥CB
∴∠AFE=∠ACB(两直线平行,同位角相等).
分析 求出∠FDE=∠2,根据平行线的判定推出DF∥AB,根据平行线的性质得出∠3=∠AEF,求出∠AEF=∠B,根据平行线的判定得出EF∥CB即可.
解答 证明:∵∠1+∠FDE=180°,∠1+∠2=180°,
∴∠FDE=∠2,
∴DF∥AB,
∴∠3=∠AEF,
∵∠3=∠B,
∴∠AEF=∠B,
∴EF∥CB,
∴∠AFE=∠ACB(两直线平行,同位角相等),
故答案为:∠FDE,∠FDE,∠2,∠AEF,∠AEF,两直线平行,同位角相等.
点评 本题考查了平行线的性质和判定的应用,能正确运用平行线的性质和判定定理进行推理是解此题的关键.

练习册系列答案
相关题目
11.下列根式中属最简二次根式的是( )
| A. | $\sqrt{{a}^{2}+1}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{{a}^{2}}$ |
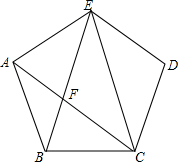 如图,正五边形ABCDE中,连接EC,AC,BE,且AC和BE交于点F,则F为AC的黄金分割点.那么△ABF和△ECF的面积之比为=$\frac{3-\sqrt{5}}{2}$.
如图,正五边形ABCDE中,连接EC,AC,BE,且AC和BE交于点F,则F为AC的黄金分割点.那么△ABF和△ECF的面积之比为=$\frac{3-\sqrt{5}}{2}$. 如图,矩形ABCD,AB=5,AD=8,E是AD上一动点,把△ABE沿BE折叠,当点A的对应点A′落在矩形ABCD的对称轴上时,折痕BE的长为$\frac{5\sqrt{5}}{2}$和$\frac{10\sqrt{3}}{3}$.
如图,矩形ABCD,AB=5,AD=8,E是AD上一动点,把△ABE沿BE折叠,当点A的对应点A′落在矩形ABCD的对称轴上时,折痕BE的长为$\frac{5\sqrt{5}}{2}$和$\frac{10\sqrt{3}}{3}$.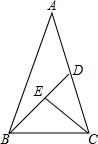 如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E.设k=$\frac{\sqrt{5}-1}{2}$,则DE=$\frac{3-\sqrt{5}}{2}$a.
如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E.设k=$\frac{\sqrt{5}-1}{2}$,则DE=$\frac{3-\sqrt{5}}{2}$a.