题目内容
3．四边形ABCD的对角线AC、BD互相平分，要使它成为矩形，需要添加的条件是AC=BD．分析 由对角线互相平分的四边形是平行四边形，得出四边形ABCD是平行四边形，再由对角线相等，即可得出结论．
解答 解：添加条件：AC=BD；理由如下：
∵四边形ABCD的对角线AC、BD互相平分，
∴四边形ABCD是平行四边形，
又∵AC=BD，
∴四边形ABCD是矩形；
故答案为：AC=BD．
点评 本题考查了平行四边形的判定、矩形的判定；熟练掌握平行四边形和矩形的判定方法是解决问题的关键．
练习册系列答案
相关题目
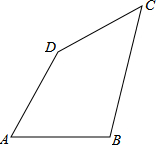如图，四边形ABCD中，AB=AD=6cm，∠A=60°，BC=3$\sqrt{5}$cm，CD=3cm，求四边形ABCD的面积．
如图，矩形ABCD，AB=5，AD=8，E是AD上一动点，把△ABE沿BE折叠，当点A的对应点A′落在矩形ABCD的对称轴上时，折痕BE的长为$\frac{5\sqrt{5}}{2}$和$\frac{10\sqrt{3}}{3}$．
11．下列根式中属最简二次根式的是（ ）
| A． | $\sqrt{{a}^{2}+1}$ | B． | $\sqrt{\frac{1}{2}}$ | C． | $\sqrt{8}$ | D． | $\sqrt{{a}^{2}}$ |
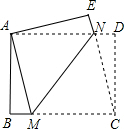如图，在矩形ABCD中，AD＞AB，将矩形ABCD折叠，使点C与点A重合，折痕为MN，折叠后再展开为矩形ABCD，连结CN．若△CDN的面积与△CMN的面积比为1：4，则$\frac{MN}{BM}$的值为2$\sqrt{6}$．
15．用反证法证明“若a⊥c，b⊥c，则a∥b”时，应假设（ ）
| A． | a不垂直于c | B． | a，b都不垂直于c | C． | a与b相交 | D． | a⊥b |
