题目内容
4.已知两实数a与b,M=a2+b2,N=2ab(1)请判断M与N的大小,并说明理由.
(2)请根据(1)的结论,求$\frac{y^2}{x^2}+\frac{x^2}{y^2}+3$的最小值(其中x,y均为正数)
(3)请判断a2+b2+c2-ab-ac-bc的正负性(a,b,c为互不相等的实数)
分析 (1)由M-N是一个完全平方式,分解因式得出M-N=(a-b)2≥0,即可得出结论;
(2)由(1)的结论容易得出结果;
(3)把原式化成=$\frac{1}{2}$[(a-b)2+(a-c)2+(b-c)2],即可得出结论.
解答 解:(1)M≥N;理由如下:
∵M-N=a2+b2-2ab=(a-b)2≥0,∴M≥N;
(2)∵$\frac{y^2}{x^2}+\frac{x^2}{y^2}+3$$≥2×\frac{y}{x}×\frac{x}{y}+3=5$
∴最小值为5;
(3)a2+b2+c2-ab-ac-bc>0,理由如下:
∵a2+b2+c2-ab-ac-bc
=$\frac{1}{2}$(2a2+2b2+2c2-2ab-2ac-2bc)
=$\frac{1}{2}$[(a-b)2+(a-c)2+(b-c)2],
∵a,b,c为互不相等的实数,
∴a2+b2+c2-ab-ac-bc>0.
点评 本题考查了因式分解的应用、偶次方的非负性质;熟练掌握用完全平方公式分解因式,并能进行推理论证是解决问题的关键.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
15.用反证法证明“若a⊥c,b⊥c,则a∥b”时,应假设( )
| A. | a不垂直于c | B. | a,b都不垂直于c | C. | a与b相交 | D. | a⊥b |
 如图,矩形ABCD,AB=5,AD=8,E是AD上一动点,把△ABE沿BE折叠,当点A的对应点A′落在矩形ABCD的对称轴上时,折痕BE的长为$\frac{5\sqrt{5}}{2}$和$\frac{10\sqrt{3}}{3}$.
如图,矩形ABCD,AB=5,AD=8,E是AD上一动点,把△ABE沿BE折叠,当点A的对应点A′落在矩形ABCD的对称轴上时,折痕BE的长为$\frac{5\sqrt{5}}{2}$和$\frac{10\sqrt{3}}{3}$.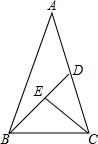 如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E.设k=$\frac{\sqrt{5}-1}{2}$,则DE=$\frac{3-\sqrt{5}}{2}$a.
如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E.设k=$\frac{\sqrt{5}-1}{2}$,则DE=$\frac{3-\sqrt{5}}{2}$a.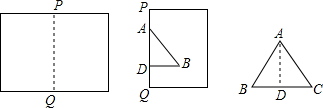
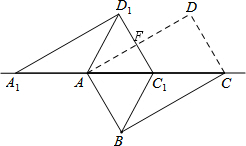 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连接AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分面积为S,则下列结论:
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连接AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分面积为S,则下列结论: