题目内容
20.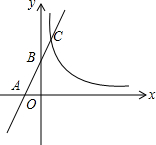 如图,已知直线与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于点C,若AB=BC,AB=2OA=2.
如图,已知直线与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于点C,若AB=BC,AB=2OA=2.(1)求点C的坐标;
(2)写出反比例函数的解析式;
(3)若点P是x轴上的一点,当△ACP是直角三角形时,求点P的坐标.
分析 (1)求出点A,B坐标进一步求出直线AB,根据相似三角形性质即可求出点C;
(2)把点C代入反比例函数求m即可;
(3)分∠APC=90°和∠ACP=90°分别求解即可.
解答 解:(1)如图1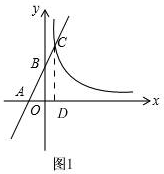
过点C作CD⊥x轴,
∴CD∥OB,
∴△AOB∽△ADC,
∴$\frac{AO}{AD}=\frac{OB}{CD}$=$\frac{AB}{AC}$,
由AB=2OA=2,可求0A=1,OB=$\sqrt{3}$,
∴A(-1,0),B(0,$\sqrt{3}$),
∵AB=BC,
∴可求CD=$2\sqrt{3}$,AD=2,OD=1,
∴C(1,$2\sqrt{3}$),
(2)把C(1,$2\sqrt{3}$)代入y=$\frac{m}{x}$,
解得m=$2\sqrt{3}$,
∴反比例函数的解析式为:$y=\frac{2\sqrt{3}}{x}$;
(3)当∠APC=90°时,由C(1,$2\sqrt{3}$)易得点P(1,0);
当∠ACP=90°时,如图2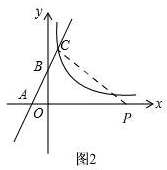
易求cos∠BAO=$\frac{1}{2}$,
在Rt△ACP中,AC=4,$\frac{AC}{AP}$=cos∠BAO=$\frac{1}{2}$,
∴AP=8,
∴OP=7,
∴点P(7,0).
点评 此题主要考查直线和反比例函数的图象问题,会运用点求函数解析式,会运用相似求线段长度,会根据条件分类讨论是解题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
1. 如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE、EC的长度分别为( )
如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE、EC的长度分别为( )
 如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE、EC的长度分别为( )
如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE、EC的长度分别为( )| A. | 1和4 | B. | 4和1 | C. | 2和3 | D. | 3和2 |
5.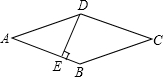 如图,菱形ABCD的周长为8cm,DE⊥AB,垂足为E,若sinA=$\frac{4}{5}$,则EB的长为( )
如图,菱形ABCD的周长为8cm,DE⊥AB,垂足为E,若sinA=$\frac{4}{5}$,则EB的长为( )
 如图,菱形ABCD的周长为8cm,DE⊥AB,垂足为E,若sinA=$\frac{4}{5}$,则EB的长为( )
如图,菱形ABCD的周长为8cm,DE⊥AB,垂足为E,若sinA=$\frac{4}{5}$,则EB的长为( )| A. | 0.4 | B. | 0.5 | C. | 0.6 | D. | 0.8 |
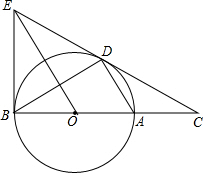 如图,D为⊙O上一点,点C在直线BA的延长线上,且∠CDA=∠CBD.
如图,D为⊙O上一点,点C在直线BA的延长线上,且∠CDA=∠CBD.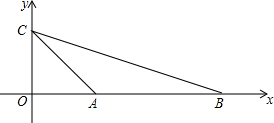 如图,已知A(1,0)、C(0,1)、B(m,0)且m>1,在平面内求一点P,使得以A、B、C、P为顶点的四边形是平行四边形,则点P的坐标为(m-1,1)或(1-m,1)或(m+1,-1).
如图,已知A(1,0)、C(0,1)、B(m,0)且m>1,在平面内求一点P,使得以A、B、C、P为顶点的四边形是平行四边形,则点P的坐标为(m-1,1)或(1-m,1)或(m+1,-1).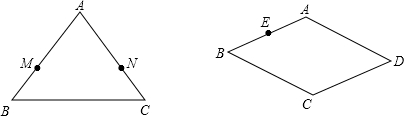
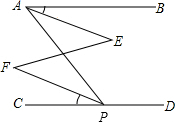 如图,∠BAP+∠APD=180°,∠BAE=∠CPF,求证:AE∥PF.
如图,∠BAP+∠APD=180°,∠BAE=∠CPF,求证:AE∥PF.