题目内容
15.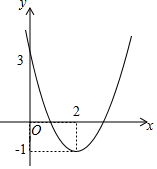 如图,已知抛物线y=ax2+bx+c的顶点为(2,-1),抛物线与y轴的交点为(0,3),当函数值y<3时,自变量x的取值范围是( )
如图,已知抛物线y=ax2+bx+c的顶点为(2,-1),抛物线与y轴的交点为(0,3),当函数值y<3时,自变量x的取值范围是( )| A. | 0<x<2 | B. | 0<x<3 | C. | 0<x<4 | D. | 1<x<3 |
分析 首先根据顶点坐标确定对称轴,然后根据对称轴和与y轴的交点坐标确定当y=3时的x的值,从而确定答案.
解答 解:∵抛物线y=ax2+bx+c的顶点为(2,-1),
∴对称轴为x=2,
∵抛物线与y轴的交点为(0,3),
∴当y=3时x的值为0或4,
∴当函数值y<3时,0<x<4,
故选C.
点评 本题考查了二次函数的性质,解题的关键是根据对称轴和与y轴的交点坐标确定当y=3时的x的值,难度不大.

练习册系列答案
相关题目
4.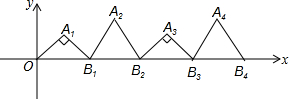 如图,在平面直角坐标系的第一象限内,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐标为(2,0),B2坐标为(4,0),B3坐标为(6,0),…,按这样的规律,点A2015的坐标是( )
如图,在平面直角坐标系的第一象限内,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐标为(2,0),B2坐标为(4,0),B3坐标为(6,0),…,按这样的规律,点A2015的坐标是( )
 如图,在平面直角坐标系的第一象限内,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐标为(2,0),B2坐标为(4,0),B3坐标为(6,0),…,按这样的规律,点A2015的坐标是( )
如图,在平面直角坐标系的第一象限内,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐标为(2,0),B2坐标为(4,0),B3坐标为(6,0),…,按这样的规律,点A2015的坐标是( )| A. | (4029,1) | B. | (2015,$\sqrt{3}$) | C. | (4030,1) | D. | (4029,$\sqrt{3}$) |
5.将235000000用科学记数法表示为( )
| A. | 235×106 | B. | 2.35×107 | C. | 2.35×108 | D. | 0.235×109 |
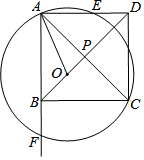 如图,正方形ABCD中,对角线 AC、BD交于点P,O为线段BP上一点(不与B、P重合),以O为圆心OA为半径作⊙O交直线AD、AB于E、F.
如图,正方形ABCD中,对角线 AC、BD交于点P,O为线段BP上一点(不与B、P重合),以O为圆心OA为半径作⊙O交直线AD、AB于E、F. 如图,已知点B,C,F,E在同一直线上,AB=DE,BC=EF,AB∥DE.求证:AC∥DF.
如图,已知点B,C,F,E在同一直线上,AB=DE,BC=EF,AB∥DE.求证:AC∥DF. 如图,已知:∠B=∠C=90°,M是BC的中点,DM平分∠ADC.
如图,已知:∠B=∠C=90°,M是BC的中点,DM平分∠ADC.