题目内容
3.已知直角三角形两边长分别是6、8,则第三边长的值是2$\sqrt{7}$或10.分析 本题已知直角三角形的两边长,但未明确这两条边是直角边还是斜边,所以求第三边的长必须分类讨论,即8是斜边或直角边的两种情况,然后利用勾股定理求解.
解答 解:当8是斜边时,第三边长=$\sqrt{{8}^{2}-{6}^{2}}$=2$\sqrt{7}$;
当6和8是直角边时,第三边长=$\sqrt{{8}^{2}+{6}^{2}}$=10;
∴第三边的长为:2$\sqrt{7}$或10,
故答案为:2$\sqrt{7}$或10.
点评 本题考查了利用勾股定理解直角三角形的能力,当已知条件中没有明确哪是斜边时,要注意讨论,一些学生往往忽略这一点,造成丢解.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
13.⊙O是等边△ABC的外接圆,⊙O的半径为4,则等边△ABC的边长为( )
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{5}$ |
15.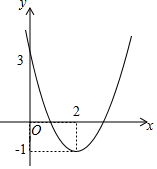 如图,已知抛物线y=ax2+bx+c的顶点为(2,-1),抛物线与y轴的交点为(0,3),当函数值y<3时,自变量x的取值范围是( )
如图,已知抛物线y=ax2+bx+c的顶点为(2,-1),抛物线与y轴的交点为(0,3),当函数值y<3时,自变量x的取值范围是( )
 如图,已知抛物线y=ax2+bx+c的顶点为(2,-1),抛物线与y轴的交点为(0,3),当函数值y<3时,自变量x的取值范围是( )
如图,已知抛物线y=ax2+bx+c的顶点为(2,-1),抛物线与y轴的交点为(0,3),当函数值y<3时,自变量x的取值范围是( )| A. | 0<x<2 | B. | 0<x<3 | C. | 0<x<4 | D. | 1<x<3 |