题目内容
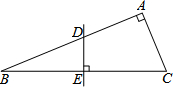 已知:在纸片上画有一直角三角形ABC,∠A=90°,∠B=22.5°,将其折叠,使点B与点C重合,折痕交AB于点D,交BC于点E,再将其打开,如图所示.若BD=3,求AB的长.
已知:在纸片上画有一直角三角形ABC,∠A=90°,∠B=22.5°,将其折叠,使点B与点C重合,折痕交AB于点D,交BC于点E,再将其打开,如图所示.若BD=3,求AB的长.考点:翻折变换(折叠问题)
专题:
分析:如图,首先证明∠DCB=∠B=22.5°,进而得到∠ADC=45°;证明AD=AC,此为解题的关键性结论;求出AD的长度,即可解决问题.
解答: 解:如图,连接DC;
解:如图,连接DC;
由题意得:DC=DB=3,
∴∠DCB=∠B=22.5°,
∴∠ADC=22.5°+22.5°=45°;
∵∠A=90°,
∴∠ACD=90°-45°=45°,
∴AD=AC(设为λ);
由勾股定理得:DC2=AD2+AC2,
即2λ2=9,解得:λ=
,
∴AB=3+
.
 解:如图,连接DC;
解:如图,连接DC;由题意得:DC=DB=3,
∴∠DCB=∠B=22.5°,
∴∠ADC=22.5°+22.5°=45°;
∵∠A=90°,
∴∠ACD=90°-45°=45°,
∴AD=AC(设为λ);
由勾股定理得:DC2=AD2+AC2,
即2λ2=9,解得:λ=
3
| ||
| 2 |
∴AB=3+
3
| ||
| 2 |
点评:该题主要考查了翻折变换的性质及其应用问题;解题的关键是灵活运用三角形的内角和定理、勾股定理等几何知识点来分析、判断、解答.

练习册系列答案
相关题目
在圆内接四边形ABCD中,∠A:∠B:∠C:∠D的度数之比可能是( )
| A、1:2:3:4 |
| B、4:2:1:3 |
| C、4:2:3:1 |
| D、1:3:2:4 |
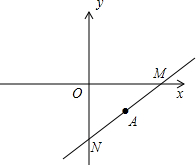 如图,已知A为直角三角形的外心,且坐标为(
如图,已知A为直角三角形的外心,且坐标为( 如图,AB=AC=9cm,BC=4cm,点A和点B关于直线l对称,AC与直线l相交于点D,则△BDC的周长是
如图,AB=AC=9cm,BC=4cm,点A和点B关于直线l对称,AC与直线l相交于点D,则△BDC的周长是 如图,在矩形ABCD中,AB=4,AD=5,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,则tan∠AFE的值为
如图,在矩形ABCD中,AB=4,AD=5,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,则tan∠AFE的值为