题目内容
解方程:(
)2-4(
)+4=0.
| x+1 |
| x2-1 |
| x+1 |
| x2-1 |
考点:换元法解分式方程
专题:
分析:根据换元法,可得一元二次方程,根据解一元二次方程,可得分式方程,根据解分式方程,可得答案.
解答:解:设u=
,原方程等价于u2-4u+4=0.解得u=2.
=2,
两边都成以(x2-1)得
x+1=2(x2-1).
因式分解,得(2x-3)(x+1)=0,
解得x=
,x=-1,
经检验:x=
是原分式方程的解,x=-1不是分式方程的解.
| x+1 |
| x2-1 |
| x+1 |
| x2-1 |
两边都成以(x2-1)得
x+1=2(x2-1).
因式分解,得(2x-3)(x+1)=0,
解得x=
| 3 |
| 2 |
经检验:x=
| 3 |
| 2 |
点评:本题考查了换元法解分式方程,把
换元成u得出一元二次方程,再求分式方程的解,注意要检验分式方程的解.
| x+1 |
| x2-1 |

练习册系列答案
相关题目
现已知线段a,b(a<b),∠MON=90°,求作Rt△ABO,使得∠O=90°,AB=b,小惠和小雷的作法分别如下.
小惠:①以点O为圆心、线段a为半径画弧,交射线ON于点A;②以点A为圆心、线段b长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
小雷:①以点O为圆心、线段a为半径画弧,交射线ON于点A;②以点O为圆心、线段b长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
则下列说法中正确的是( )
小惠:①以点O为圆心、线段a为半径画弧,交射线ON于点A;②以点A为圆心、线段b长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
小雷:①以点O为圆心、线段a为半径画弧,交射线ON于点A;②以点O为圆心、线段b长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
则下列说法中正确的是( )
| A、小惠的作法正确,小雷的作法错误 |
| B、小雷的作法正确,小惠的作法错误 |
| C、两人的作法都正确 |
| D、两人的作法都错误 |
下列说法中不正确的是( )
| A、经过平移,图形对应点连成的线段平行且相等 |
| B、平移中,图形上每个点移动的距离不同 |
| C、经过平移,图形的对应线段,对应角分别相等 |
| D、平移不改变图形的形状和大小 |
已知
是方程mx+2y=2的一个解,那么m为( )
|
| A、4 | ||
B、
| ||
| C、-4 | ||
| D、1 |
下列以x=0为解的方程是( )
| A、x(x-2)=4 | ||
| B、3-(x-1)=4 | ||
| C、2x-1=4-3x | ||
D、
|
 如图,在△ABD中,∠A=∠B=30°,以AB边上一点O为圆心,过A,D两点作⊙O交AB于C.
如图,在△ABD中,∠A=∠B=30°,以AB边上一点O为圆心,过A,D两点作⊙O交AB于C.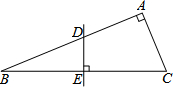 已知:在纸片上画有一直角三角形ABC,∠A=90°,∠B=22.5°,将其折叠,使点B与点C重合,折痕交AB于点D,交BC于点E,再将其打开,如图所示.若BD=3,求AB的长.
已知:在纸片上画有一直角三角形ABC,∠A=90°,∠B=22.5°,将其折叠,使点B与点C重合,折痕交AB于点D,交BC于点E,再将其打开,如图所示.若BD=3,求AB的长.