题目内容
3．
如图，已知△ABC的两条高BF，CE交于点H，∠BAC=65°，求∠BHC的度数．
分析 根据三角形的搞定概念得到∠AEH=90°，∠AFH=90°，根据是不想的内角和等于360°计算即可．
解答 解：∵BF，CE是△ABC的两条高，
∴∠AEH=90°，∠AFH=90°，又∠BAC=65°，
∴∠EHF=360°-90°-90°-65°=125°，
∴∠BHC=∠EHF=125°．
点评 本题考查的是三角形的内角和定理，掌握三角形的内角和等于180°是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
16．某电信公司给顾客提供了A、B、C三种宽带上网的收费方式：
设某用户每月的上网时间为x（小时），A、B、C三种收费方式的收费金额分别为y1、y2、y3（元）．
（1）分别求y1、y1、y2关于x的函数关系式，并写出相应的自变量的取值范围；
（2）请你帮该用户选择较省钱的收费方式，并说明理由．
| 收费方式 | 月使用费/元 | 包时上网时间/小时 | 超时费/（元/分钟） |
| A | 30 | 25 | 0.05 |
| B | 50 | 50 | 0.05 |
| C | 120 | 不限时 |
（1）分别求y1、y1、y2关于x的函数关系式，并写出相应的自变量的取值范围；
（2）请你帮该用户选择较省钱的收费方式，并说明理由．
如图，黑板上的题目小明不会做，请你帮他填上x=0或x=7．
如图，△ABC中，CE平分∠ACB，CF平分∠ACD，且EF∥BC交AC于M，若EF=5，则CE2+CF2=25．
15．
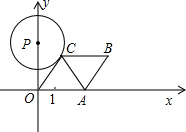如图所示，已知A点从（1，0）点出发，以每秒1个单位长的速度沿着x轴的正方向运动，经过t秒后，以O、A为顶点作菱形OABC，使B．C点都在第一象限内，且AO=AC，又以P（0，4$\sqrt{3}$）为圆心，PC为半径的圆恰好与OC所在的直线相切，则t=（ ）
如图所示，已知A点从（1，0）点出发，以每秒1个单位长的速度沿着x轴的正方向运动，经过t秒后，以O、A为顶点作菱形OABC，使B．C点都在第一象限内，且AO=AC，又以P（0，4$\sqrt{3}$）为圆心，PC为半径的圆恰好与OC所在的直线相切，则t=（ ）| A． | 2$\sqrt{3}$-1 | B． | 2$\sqrt{3}$+1 | C． | 5 | D． | 7 |
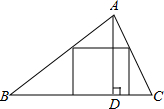如图，△ABC是一块锐角三角形材料，边BC=80mm，高AD=60mm，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是$\frac{240}{7}$mm．