题目内容
18. 如图,△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若EF=5,则CE2+CF2=25.
如图,△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若EF=5,则CE2+CF2=25.
分析 根据角平分线的定义推出△ECF为直角三角形,然后根据勾股定理即可求得CE2+CF2=EF2,进而可求出CE2+CF2的值.
解答 解:∵CE平分∠ACB,CF平分∠ACD,
∴∠ACE=$\frac{1}{2}$∠ACB,∠ACF=$\frac{1}{2}$∠ACD,
∴∠ECF=$\frac{1}{2}$(∠ACB+∠ACD)=90°,
∴△EFC为直角三角形,
由勾股定理可知CE2+CF2=EF2=25.
故答案为:25.
点评 本题考查角平分线的定义,直角三角形的判定以及勾股定理的运用,解题的关键是首先证明出△ECF为直角三角形.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
9.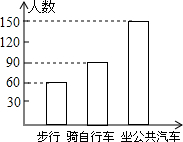 如图,下列说法正确的是( )
如图,下列说法正确的是( )
 如图,下列说法正确的是( )
如图,下列说法正确的是( )| A. | 步行人数最少,只为90人 | |
| B. | 步行人数为50人 | |
| C. | 步行与骑自行车的人数和比坐公共汽车的人数要多 | |
| D. | 坐公共汽车的人数占总数的50% |
13.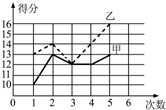 甲、乙两人参加某体育项目训练,为了便于了解他们的训练情况,教练将他们最近五次的训练成绩用如图所示的复式统计图表示出来,则下面结论错误的是( )
甲、乙两人参加某体育项目训练,为了便于了解他们的训练情况,教练将他们最近五次的训练成绩用如图所示的复式统计图表示出来,则下面结论错误的是( )
 甲、乙两人参加某体育项目训练,为了便于了解他们的训练情况,教练将他们最近五次的训练成绩用如图所示的复式统计图表示出来,则下面结论错误的是( )
甲、乙两人参加某体育项目训练,为了便于了解他们的训练情况,教练将他们最近五次的训练成绩用如图所示的复式统计图表示出来,则下面结论错误的是( )| A. | 甲的第三次成绩与第四次成绩相同 | |
| B. | 第三次训练,甲、乙两人的成绩相同 | |
| C. | 第四次训练,甲的成绩比乙的成绩少2分 | |
| D. | 五次训练,甲的成绩都比乙的成绩高 |
10. 如图几何体从正面看是( )
如图几何体从正面看是( )
 如图几何体从正面看是( )
如图几何体从正面看是( )| A. |  | B. |  | C. |  | D. |  |
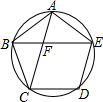 如图所示,正五边形ABCDE的对角线AC和BE相交于点F,求证:AC=AB+BF.
如图所示,正五边形ABCDE的对角线AC和BE相交于点F,求证:AC=AB+BF. 如图,已知△ABC的两条高BF,CE交于点H,∠BAC=65°,求∠BHC的度数.
如图,已知△ABC的两条高BF,CE交于点H,∠BAC=65°,求∠BHC的度数.