题目内容
12.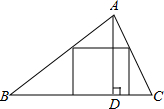 如图,△ABC是一块锐角三角形材料,边BC=80mm,高AD=60mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是$\frac{240}{7}$mm.
如图,△ABC是一块锐角三角形材料,边BC=80mm,高AD=60mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是$\frac{240}{7}$mm.
分析 如图,设正方形EFGH的边长为x,EF与AD交于点K.由EF∥BC,得到△AEF∽△ABC,得到$\frac{EF}{BC}$=$\frac{AK}{AD}$,得$\frac{x}{80}$=$\frac{60-x}{60}$,列方程即可.
解答 解:如图,设正方形EFGH的边长为x,EF与AD交于点K.
∵EF∥BC,
∴△AEF∽△ABC,
∴$\frac{EF}{BC}$=$\frac{AK}{AD}$,
∴$\frac{x}{80}$=$\frac{60-x}{60}$,
∴x=$\frac{240}{7}$,
故答案为$\frac{240}{7}$.
点评 本题考查相似三角形的应用,解题的关键是熟练掌握相似三角形的应用,属于基础题中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.在数轴上a所对应的点与b所对应的点相差6个单位长度,若-a=2,则b等于( )
| A. | 4 | B. | -4 | C. | -8 | D. | 4或-8 |
 如图,已知△ABC的两条高BF,CE交于点H,∠BAC=65°,求∠BHC的度数.
如图,已知△ABC的两条高BF,CE交于点H,∠BAC=65°,求∠BHC的度数.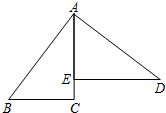 如图,AB=AD,∠BAD=90°,AC⊥BC于点C,DE⊥AC于点E,且AB=5,BC=3,则CE=1.
如图,AB=AD,∠BAD=90°,AC⊥BC于点C,DE⊥AC于点E,且AB=5,BC=3,则CE=1. 杭州市推行垃圾分类已经多年,但在厨余垃圾中除了厨余类垃圾还混杂着非厨余类垃圾,如图是杭州市某一天收到的厨余垃圾的统计图,则m的值为69.01.
杭州市推行垃圾分类已经多年,但在厨余垃圾中除了厨余类垃圾还混杂着非厨余类垃圾,如图是杭州市某一天收到的厨余垃圾的统计图,则m的值为69.01.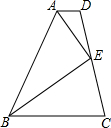 已知:如图,AD∥BC,点E是DC的中点,BE平分∠ABC,求证:AE平分∠BAD.
已知:如图,AD∥BC,点E是DC的中点,BE平分∠ABC,求证:AE平分∠BAD.