题目内容
2．
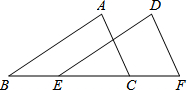如图，点B、E、C、F在同一条直线上，且BE=CF，AB∥DE，AC∥DF，求证：AB=DE．
分析 先求出BC=EF，再根据两直线平行，同位角相等求出∠B=∠DEF，∠ACB=∠F，然后利用“角边角”证明△ABC和△DEF全等，根据全等三角形对应边相等证明即可．
解答 证明：∵BE=CF，
∴BE+EC=CF+EC，
即BC=EF，
∵AB∥DE，
∴∠B=∠DEF，
∵AC∥DF，
∴∠ACB=∠F，
在△ABC和△DEF中，$\left\{\begin{array}{l}{∠B=∠DEF}\\{BC=EF}\\{∠ACB=∠F}\end{array}\right.$，
∴△ABC≌△DEF（ASA），
∴AB=DE．
点评 本题考查了全等三角形的判定与性质，平行线的性质，熟练掌握三角形全等的判定方法是解题的关键．
练习册系列答案
相关题目
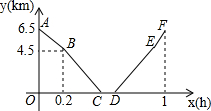从甲地到乙地，先是一段上坡路，然后是一段平路，小明骑车从甲地出发，到达乙地后休息一段时间，然后原路返回甲地，假设小明骑车在上坡、平路、下坡时分别保持匀速前进，已知小明骑车上坡的速度比平路上的速度每小时少5km，下坡的速度比在平路上的速度每小时多5km，小明出发时间为x（单位：h），距乙地的距离为y（单位：km），图中的折线ABCDEF表示y与x之间的函数关系．
在平面直角坐标系中，A（3，3）、B（3，1）、C（5，0）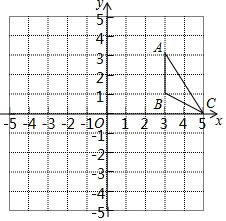
如图，在平面直角坐标系中，A（3，3），B（3，1），C（5，0）．
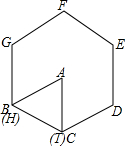正△ABC与正六边形DEFGH的边长相等，初始如图所示，将三角形绕点I顺时针旋转使得AC与CD重合，再将三角形绕点D顺时针旋转使得AB与DE重合，…，按这样的方式将△ABC旋转2015次后，△ABC中与正六边形DEFGHI重合的边是（ ）
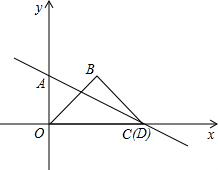如图，在平面直角坐标系xOy中，已知直线AC的解析式为y=-$\frac{1}{4}$x+1，直线AC交x轴于点C，交y轴于点A．