题目内容
11.化简下列各题:(1)3a-[-3b+4a-2(a-b)]
(2)2a2-2[-ab+3a2-($\frac{1}{2}$a2-3ab)].
分析 (1)先去括号,再合并同类项即可;
(2)先去括号,再合并同类项即可.
解答 解:(1)3a-[-3b+4a-2(a-b)]
=3a-[-3b+4a-2a+2b]
=3a+3b-4a+2a-2b
=a+b;
(2)2a2-2[-ab+3a2-($\frac{1}{2}$a2-3ab)]
=2a2-2[-ab+3a2-$\frac{1}{2}$a2+3ab]
=2a2+2ab-6a2+a2-6ab
=-3a2-4ab.
点评 本题考查的是整式的加减,熟知整式的加减实质上是去括号、合并同类项是解答此题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
16.五边形的对角线共有( )条.
| A. | 2 | B. | 4 | C. | 5 | D. | 6 |
3.下列各组中的三条线段不能组成三角形的是( )
| A. | 3,3,3 | B. | 4,4,8 | C. | 3,4,5 | D. | 6,6,11 |
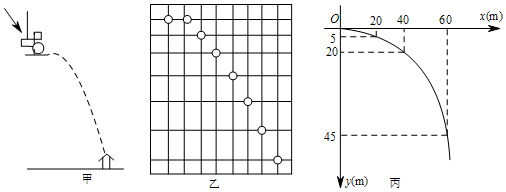
20.物理实验过程:如图甲所示,以初始速度v0(m/s)用小锤击打弱性金属片,不考虑空气阻力时,小球做平抛运动.用频闪照相的方法观测到小球在下落过程中的几个位置(图乙),用平滑曲线把这些位置连起来,就得到平抛运动的轨迹(图丙).
数学问题:在图丙中,以小球被击出的水平方向为x轴正方向,竖直向下的方向为y轴正方向,小球被击出点为原点建立直角坐标系,得到小球的位置坐标(x,y)(x>0,y>0).由物理知识可得到x(m),y(m)与时间t(s)的关系如下:①x=v0t;②y=$\frac{1}{2}$gt2.
由实验测得3个时刻小球的位置坐标如下表所示.
(1)v0=20m/s,g=10m/s2.
(2)求出y与x之间的函数关系式.
(3)当小球在竖直方向上下落80m时,它在水平方向上前进了多少?
数学问题:在图丙中,以小球被击出的水平方向为x轴正方向,竖直向下的方向为y轴正方向,小球被击出点为原点建立直角坐标系,得到小球的位置坐标(x,y)(x>0,y>0).由物理知识可得到x(m),y(m)与时间t(s)的关系如下:①x=v0t;②y=$\frac{1}{2}$gt2.
由实验测得3个时刻小球的位置坐标如下表所示.
| t(s) | 1 | 2 | 3 |
| x(m) | 20 | 40 | 60 |
| y(m) | 5 | 20 | 45 |

(1)v0=20m/s,g=10m/s2.
(2)求出y与x之间的函数关系式.
(3)当小球在竖直方向上下落80m时,它在水平方向上前进了多少?
 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).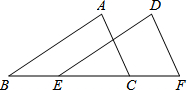 如图,点B、E、C、F在同一条直线上,且BE=CF,AB∥DE,AC∥DF,求证:AB=DE.
如图,点B、E、C、F在同一条直线上,且BE=CF,AB∥DE,AC∥DF,求证:AB=DE.