题目内容
10.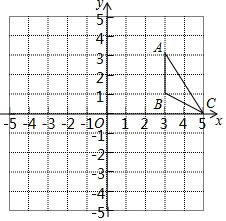 如图,在平面直角坐标系中,A(3,3),B(3,1),C(5,0).
如图,在平面直角坐标系中,A(3,3),B(3,1),C(5,0).(1)将△ABC向左平移6个单位得到△A1B1C1,画出△A1B1C1;
(2)将△A1B1C1绕点C1逆时针方向旋转90°,直接写出线段A1C1所扫过图形的面积.
分析 (1)将△ABC的三顶点分别向左平移6个单位得到对应点,顺次连接即可得;
(2)由旋转的性质得旋转角为90度,利用扇形面积公式求解即可.
解答 解:(1)如图,△A1B1C1即为所求;
(2)如图,旋转后所得三角形为△A2B2C1,
∵A1C1=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
则线段A1C1所扫过图形的面积为$\frac{90•π•(\sqrt{13})^{2}}{360}$=$\frac{13}{4}$π.
点评 本题主要考查作图-旋转变换和平移变换,熟练掌握旋转变换和平移变换的性质及扇形面积公式是解题的关键.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
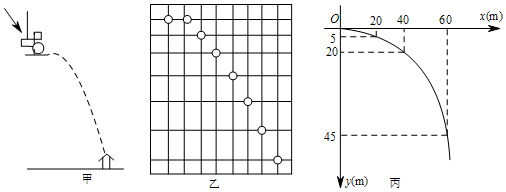
20.物理实验过程:如图甲所示,以初始速度v0(m/s)用小锤击打弱性金属片,不考虑空气阻力时,小球做平抛运动.用频闪照相的方法观测到小球在下落过程中的几个位置(图乙),用平滑曲线把这些位置连起来,就得到平抛运动的轨迹(图丙).
数学问题:在图丙中,以小球被击出的水平方向为x轴正方向,竖直向下的方向为y轴正方向,小球被击出点为原点建立直角坐标系,得到小球的位置坐标(x,y)(x>0,y>0).由物理知识可得到x(m),y(m)与时间t(s)的关系如下:①x=v0t;②y=$\frac{1}{2}$gt2.
由实验测得3个时刻小球的位置坐标如下表所示.
(1)v0=20m/s,g=10m/s2.
(2)求出y与x之间的函数关系式.
(3)当小球在竖直方向上下落80m时,它在水平方向上前进了多少?
数学问题:在图丙中,以小球被击出的水平方向为x轴正方向,竖直向下的方向为y轴正方向,小球被击出点为原点建立直角坐标系,得到小球的位置坐标(x,y)(x>0,y>0).由物理知识可得到x(m),y(m)与时间t(s)的关系如下:①x=v0t;②y=$\frac{1}{2}$gt2.
由实验测得3个时刻小球的位置坐标如下表所示.
| t(s) | 1 | 2 | 3 |
| x(m) | 20 | 40 | 60 |
| y(m) | 5 | 20 | 45 |

(1)v0=20m/s,g=10m/s2.
(2)求出y与x之间的函数关系式.
(3)当小球在竖直方向上下落80m时,它在水平方向上前进了多少?
 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).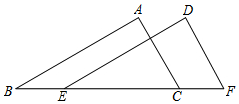 如图,在△ABC和△DEF中,B、E、C、F在同一直线上,已知AB=DE,AC=DF,BE=CF.求证:AB∥DE.
如图,在△ABC和△DEF中,B、E、C、F在同一直线上,已知AB=DE,AC=DF,BE=CF.求证:AB∥DE. 如图,m∥n,等边△ABC的顶点B在直线n上,边AC交直线m于D,∠1=25°,则∠2的度数为35°.
如图,m∥n,等边△ABC的顶点B在直线n上,边AC交直线m于D,∠1=25°,则∠2的度数为35°. 正八边形ABCDEFGH的半径为$\sqrt{2}$cm,则它的面积为8$\sqrt{2}$cm2.
正八边形ABCDEFGH的半径为$\sqrt{2}$cm,则它的面积为8$\sqrt{2}$cm2.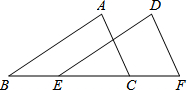 如图,点B、E、C、F在同一条直线上,且BE=CF,AB∥DE,AC∥DF,求证:AB=DE.
如图,点B、E、C、F在同一条直线上,且BE=CF,AB∥DE,AC∥DF,求证:AB=DE.