题目内容
15.(1)解方程:${x}^{2}-2\sqrt{5}x+1=0$(2)计算:($\sqrt{2}$+1)($\sqrt{2}$-1)-($\sqrt{3}$-2)2.
分析 (1)直接利用公式法解方程得出答案;
(2)直接利用乘法公式化简二次根式求出答案.
解答 解:(1)${x}^{2}-2\sqrt{5}x+1=0$
△=b2-4ac=20-4=16,
则x=$\frac{2\sqrt{5}±\sqrt{16}}{2}$=$\sqrt{5}$±2,
故x1=$\sqrt{5}$+2,x2=$\sqrt{5}$-2;
(2)($\sqrt{2}$+1)($\sqrt{2}$-1)-($\sqrt{3}$-2)2
=2-1-(3+4-4$\sqrt{3}$)
=1-7+4$\sqrt{3}$
=-6+4$\sqrt{3}$.
点评 此题主要考查了二次根式的混合运算,正确应用乘法公式是解题关键.

练习册系列答案
相关题目
4.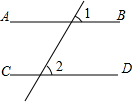 如图,由∠1=∠2得到AB∥CD的理由是( )
如图,由∠1=∠2得到AB∥CD的理由是( )
 如图,由∠1=∠2得到AB∥CD的理由是( )
如图,由∠1=∠2得到AB∥CD的理由是( )| A. | 两直线平行,同位角相等 | B. | 两直线平行,内错角相等 | ||
| C. | 同位角相等,两直线平行 | D. | 内错角相等,两直线平行 |