题目内容
在下列四个图形中，△DEF能由△ABC经过平移得到的图形是（ ）
A、 |
B、 |
C、 |
D、 |
考点：平移的性质
专题：
分析：根据图形平移的性质对各选项进行逐一分析即可．
解答：解：A、△DEF由△ABC位似变换而成，故本选项错误．
B、△DEF由△ABC平移而成，故本选项正确；
C、△DEF由△ABC对称而成，故本选项错误；
D、△DEF由△ABC旋转而成，故本选项错误；
故选B．
B、△DEF由△ABC平移而成，故本选项正确；
C、△DEF由△ABC对称而成，故本选项错误；
D、△DEF由△ABC旋转而成，故本选项错误；
故选B．
点评：本题考查的是平移的性质，熟知把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同是解答此题的关键．
练习册系列答案
相关题目
刘强在作业中的一道题：如图1，直线a，b所成的角跑到画板外面去了，你有什么办法量出这两条直线所成的角的度数？刘强的做法是：如图2，画PC∥a，量出直线b与PC的夹角度数，即直线a，b所成角的度数．其依据是（ ）
| A、同位角相等，两直线平行 |
| B、同旁内角互补，两直线平行 |
| C、内错角相等，两直线平行 |
| D、两直线平行，同位角相等 |
有一直角三角形的两边长分别为3和4，则第三边长是（ ）
| A、5 | ||
B、5或
| ||
C、
| ||
D、
|
化简
的结果是（ ）
| -a3b2c |
| ab |
| A、-a2b |
| B、-a2c |
| C、-a2bc |
| D、-bc |
如图，已知AB∥CD，∠BAE=100°，∠C=120°，则∠1=（ ）| A、80° | B、60° |
| C、40° | D、20° |
如果两条平行线被第三条直线所截，那么其中一组同位角的角平分线（ ）
| A、垂直 | B、相交 |
| C、平行 | D、不能确定 |
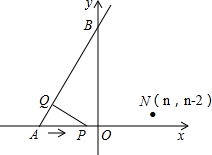如图，已知射线AB与x轴和y轴分别交于点A（-3，0）和点B（0，3