题目内容
 如图,在直角三角形中,两直角边长为a,b斜边上的高为h,判断以ab,ah,bh为边长的三角形形状并说明理由.
如图,在直角三角形中,两直角边长为a,b斜边上的高为h,判断以ab,ah,bh为边长的三角形形状并说明理由.考点:勾股定理的逆定理
专题:
分析:首先设斜边长为c,根据勾股定理可得a2+b2=c2,再根据直角三角形的面积可得ab=ch,然后再利用勾股定理逆定理证明三角形是直角三角形.
解答:解:设斜边长为c,
∵三角形是直角三角形,
∴a2+b2=c2,
:∵
ab=
ch
∴ab=ch,
∵(ah)2+(bh)2=a2h2+b2h2=(a2+b2)h2=c2h2=(ch)2=(ab)2.
∴三角形是直角三角形.
∵三角形是直角三角形,
∴a2+b2=c2,
:∵
| 1 |
| 2 |
| 1 |
| 2 |
∴ab=ch,
∵(ah)2+(bh)2=a2h2+b2h2=(a2+b2)h2=c2h2=(ch)2=(ab)2.
∴三角形是直角三角形.
点评:此题主要考查了勾股定理逆定理,关键是掌握勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
相关题目
有一直角三角形的两边长分别为3和4,则第三边长是( )
| A、5 | ||
B、5或
| ||
C、
| ||
D、
|
下面计算正确的是( )
| A、b3b2=b6 |
| B、x3+x3=x6 |
| C、a4+a2=a6 |
| D、mm5=m6 |
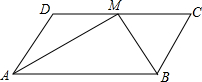 如图,在平行四边形ABCD中,M是CD的中点,AB=2BC,BM=a,AM=b,则CD的长为( )
如图,在平行四边形ABCD中,M是CD的中点,AB=2BC,BM=a,AM=b,则CD的长为( )A、
| ||
B、a+
| ||
C、
| ||
D、
|
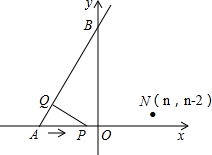 如图,已知射线AB与x轴和y轴分别交于点A(-3,0)和点B(0,3
如图,已知射线AB与x轴和y轴分别交于点A(-3,0)和点B(0,3