题目内容
9.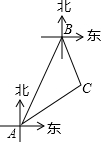 如图,点A、B是两个相距4000米的海岸观察点,点B位于点A的北偏东30°方向上,某日两观察点同时收到海面上的船C发出的信号,此时测得船C位于点A的北偏东60°方向上,位于点B的南偏东15°方向上,求此时船C到海岸AB的距离.(参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1米)
如图,点A、B是两个相距4000米的海岸观察点,点B位于点A的北偏东30°方向上,某日两观察点同时收到海面上的船C发出的信号,此时测得船C位于点A的北偏东60°方向上,位于点B的南偏东15°方向上,求此时船C到海岸AB的距离.(参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1米)
分析 过C作CD⊥AB于D,根据已知条件得到∠BAC=30°,∠ABC=45°,解直角三角形得到AD=$\frac{CD}{tan30°}$=$\frac{CD}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$CD,BD=CD,列方程即可得结论.
解答 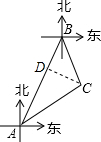 解:过C作CD⊥AB于D,
解:过C作CD⊥AB于D,
根据题意得:∠BAC=30°,∠ABC=45°,
在Rt△ACD中,AD=$\frac{CD}{tan30°}$=$\frac{CD}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$CD,
在Rt△BCD中,BD=CD,
∵AB=AD+BD=$\sqrt{3}$CD+CD=4000,
∴CD=2000($\sqrt{3}$-1)≈732.0米.
答:船C到海岸AB的距离大约为732.0米.
点评 本题考查了解直角三角形的应用-方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键.

练习册系列答案
相关题目
4.求一个数的立方根,有些数可以直接求得,如$\root{3}{8}$,有些数则不能直接求得,如$\root{3}{5}$,但可以通过计算器求得.还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
(1)表中所给的信息中,你能发现什么规律?(请将规律用文字表达出来)
(2)运用你发现的规律,探究下列问题:
已知$\root{3}{2.5}$≈1.36,求下列各数的立方根:
①0.0025; ②2500000.
| n | 8 | 0.008 | 0.000008 | 8000 | 8000000 | … |
| $\root{3}{n}$ | 2 | 0.2 | 0.02 | 20 | 200 | … |
(2)运用你发现的规律,探究下列问题:
已知$\root{3}{2.5}$≈1.36,求下列各数的立方根:
①0.0025; ②2500000.
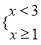 的解集在数轴上表示为
的解集在数轴上表示为 ( )
( )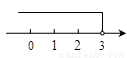 B.
B. 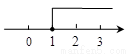 C.
C. 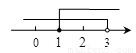 D.
D. 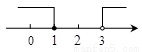
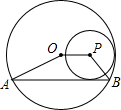 如图,⊙P内切于⊙O,⊙O的弦AB与⊙P相切,且AB∥OP,若⊙O的半径为3,⊙P的半径为1,则四边形ABPO的面积为2$+2\sqrt{2}$.
如图,⊙P内切于⊙O,⊙O的弦AB与⊙P相切,且AB∥OP,若⊙O的半径为3,⊙P的半径为1,则四边形ABPO的面积为2$+2\sqrt{2}$.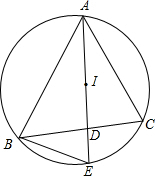 如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC外接圆于点E.
如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC外接圆于点E.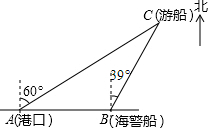 如图,一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东39°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(结果精确到0.01小时)
如图,一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东39°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(结果精确到0.01小时)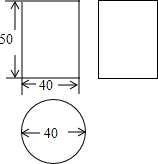 某工厂接受了加工100件密封罐的任务,设计者给出了密封罐的三视图(如图所示,单位:cm),已知加工这种密封罐需全部用铁皮焊接,那么该工厂至少要准备多少平方米的铁皮?
某工厂接受了加工100件密封罐的任务,设计者给出了密封罐的三视图(如图所示,单位:cm),已知加工这种密封罐需全部用铁皮焊接,那么该工厂至少要准备多少平方米的铁皮?