题目内容
16.计算:(1)3$\sqrt{40}$-$\sqrt{\frac{2}{5}}$-2$\sqrt{\frac{1}{10}}$;
(2)$\sqrt{12}$+$\sqrt{\frac{1}{27}}$$-\sqrt{\frac{1}{3}}$;
(3)x$\sqrt{\frac{1}{x}}$+$\sqrt{4y}$-$\frac{\sqrt{x}}{2}$+y$\sqrt{\frac{1}{y}}$;
(4)$\sqrt{0.8}$-$\frac{1}{4}$($\sqrt{3.2}$+2$\sqrt{180}$)
分析 (1)各项化为最简后,合并同类二次根式;
(2)各项化为最简,然后合并同类二次根式;
(3)各项化为最简后,合并同类二次根式;
(4)各项化为最简后,去括号,合并同类二次根式.
解答 解:(1)3$\sqrt{40}$-$\sqrt{\frac{2}{5}}$-2$\sqrt{\frac{1}{10}}$
=6$\sqrt{10}$-$\frac{1}{5}$$\sqrt{10}$-$\frac{1}{5}$$\sqrt{10}$
=$\frac{28}{5}$$\sqrt{10}$;
(2)$\sqrt{12}$+$\sqrt{\frac{1}{27}}$$-\sqrt{\frac{1}{3}}$
=2$\sqrt{3}$+$\frac{1}{9}$$\sqrt{3}$-$\frac{1}{3}$$\sqrt{3}$
=$\frac{16}{9}$$\sqrt{3}$;
(3)x$\sqrt{\frac{1}{x}}$+$\sqrt{4y}$-$\frac{\sqrt{x}}{2}$+y$\sqrt{\frac{1}{y}}$
=$\sqrt{x}$+2$\sqrt{y}$-$\frac{\sqrt{x}}{2}$+$\sqrt{y}$
=$\frac{1}{2}$$\sqrt{x}$+3$\sqrt{y}$;
(4)$\sqrt{0.8}$-$\frac{1}{4}$($\sqrt{3.2}$+2$\sqrt{180}$)
=$\frac{2}{5}$$\sqrt{5}$-$\frac{1}{5}$$\sqrt{5}$-3$\sqrt{5}$
=-$\frac{14}{5}$$\sqrt{5}$.
点评 此题考查了二次根式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
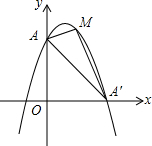 已知,抛物线y=-x2+2x+3与y轴交于A点与x轴正半轴交于A′,点M为第一象限内抛物线上的一动点,问:点M在何处时,△AMA′的面积最大,最大面积为多少.
已知,抛物线y=-x2+2x+3与y轴交于A点与x轴正半轴交于A′,点M为第一象限内抛物线上的一动点,问:点M在何处时,△AMA′的面积最大,最大面积为多少.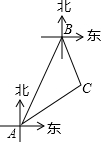 如图,点A、B是两个相距4000米的海岸观察点,点B位于点A的北偏东30°方向上,某日两观察点同时收到海面上的船C发出的信号,此时测得船C位于点A的北偏东60°方向上,位于点B的南偏东15°方向上,求此时船C到海岸AB的距离.(参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1米)
如图,点A、B是两个相距4000米的海岸观察点,点B位于点A的北偏东30°方向上,某日两观察点同时收到海面上的船C发出的信号,此时测得船C位于点A的北偏东60°方向上,位于点B的南偏东15°方向上,求此时船C到海岸AB的距离.(参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1米)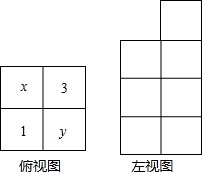 如图是由几何小立方体搭成的几何体的俯视图,正方形中的数字和字母表示叠在该位置上的小正方体的个数,再根据左视图,求x,y的值,并画出此时的主视图.
如图是由几何小立方体搭成的几何体的俯视图,正方形中的数字和字母表示叠在该位置上的小正方体的个数,再根据左视图,求x,y的值,并画出此时的主视图.