题目内容
20.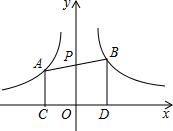 如图,直线分别与反比例函数y=-$\frac{2}{x}$和y=$\frac{3}{x}$的图象交于点A和点B,与y轴交于点P,且P为线段AB的中点,作AC⊥x轴于点C,BD⊥x于点D,则四边形ABDC的面积是( )
如图,直线分别与反比例函数y=-$\frac{2}{x}$和y=$\frac{3}{x}$的图象交于点A和点B,与y轴交于点P,且P为线段AB的中点,作AC⊥x轴于点C,BD⊥x于点D,则四边形ABDC的面积是( )| A. | 3.5 | B. | 4 | C. | 4.5 | D. | 5 |
分析 由已知条件得到AC∥PO∥BD,推出OC=OD,设A(-m,$\frac{2}{m}$),B(m,$\frac{3}{m}$),得到AC=$\frac{2}{m}$,BD=$\frac{3}{m}$,CD=2m,根据梯形的面积公式即可得到结论.
解答 解:∵AC⊥x轴于点C,BD⊥x于点D,
∴AC∥PO∥BD,
∵P为线段AB的中点,
∴OC=OD,
设A(-m,$\frac{2}{m}$),B(m,$\frac{3}{m}$),
∴AC=$\frac{2}{m}$,BD=$\frac{3}{m}$,CD=2m,
∴四边形ABDC的面积=$\frac{1}{2}$(AC+BD)•CD=$\frac{1}{2}$($\frac{2}{m}+\frac{3}{m}$)•2m=5,
故选D.
点评 本题考查了反比例函数系数k的几何意义,平行线等分线段定理,梯形的面积的计算,熟练掌握平行线等分线段定理是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 如图,电信部门计划修建一条连接B、C两地电缆,测量人员在山脚A处测得B、C两处的仰角分别是37°和45°,在B处测得C处的仰角为67°.已知C地比A地髙330米(图中各点均在同一平面内),求电缆BC长至少多少米?(精确到米,参考数据:sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin67°≈$\frac{12}{13}$,tan67°≈$\frac{12}{5}$)
如图,电信部门计划修建一条连接B、C两地电缆,测量人员在山脚A处测得B、C两处的仰角分别是37°和45°,在B处测得C处的仰角为67°.已知C地比A地髙330米(图中各点均在同一平面内),求电缆BC长至少多少米?(精确到米,参考数据:sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin67°≈$\frac{12}{13}$,tan67°≈$\frac{12}{5}$) 解不等式组$\left\{\begin{array}{l}2x-1≤x+2,①\\ \frac{3x+1}{5}+2≥1.②\end{array}\right.$请结合题意填空,完成本题的解答.
解不等式组$\left\{\begin{array}{l}2x-1≤x+2,①\\ \frac{3x+1}{5}+2≥1.②\end{array}\right.$请结合题意填空,完成本题的解答.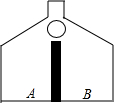 现有一游戏装置如图所示,小球从最上方入口处投入,每次遇到黑色障碍物后,等可能地向左、右两边落下.
现有一游戏装置如图所示,小球从最上方入口处投入,每次遇到黑色障碍物后,等可能地向左、右两边落下.