题目内容
12.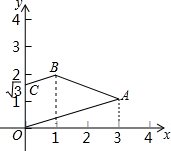 如图,A,B,C三点的坐标分别为(3,1),(1,2),(0,$\sqrt{3}$),试求四边形OABC的面积.
如图,A,B,C三点的坐标分别为(3,1),(1,2),(0,$\sqrt{3}$),试求四边形OABC的面积.
分析 用一个五边的面积减去一个三角形的面积得到四边形OABC的面积,而五边形的面积可分为两个直角梯形的面积,然后根据三角形和梯形的面积公式计算.
解答 解:四边形OABC的面积=$\frac{1}{2}$×($\sqrt{3}$+2)×1+$\frac{1}{2}$×(1+2)×2-$\frac{1}{2}$×1×3=$\frac{5+\sqrt{3}}{2}$.
点评 本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系.也考查了梯形和三角形的面积公式.

练习册系列答案
相关题目
2.下列事件为必然事件的是( )
| A. | 如果a,b是实数,那么a•b=b•a | |
| B. | 抛掷一枚均匀的硬币,落地后正面朝上 | |
| C. | 汽车行驶到交通岗遇到绿色的信号灯 | |
| D. | 口袋中装有3个红球,从中随机摸出一球,这个球是白球 |
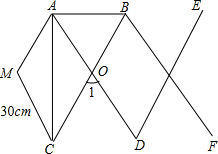 某厂要生产一批边长为30cm的菱形衣帽架(如图),若∠1=60°,则AB,AC的长各是多少?
某厂要生产一批边长为30cm的菱形衣帽架(如图),若∠1=60°,则AB,AC的长各是多少?