题目内容
7.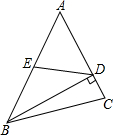 如图,在△ABC中,BD⊥AC于D,点E为AB的中点,AD=6,DE=5,则线段BD的长等于8.
如图,在△ABC中,BD⊥AC于D,点E为AB的中点,AD=6,DE=5,则线段BD的长等于8.
分析 利用直角三角形斜边上的中线等于斜边的一半,进而结合勾股定理得出BD的长.
解答 解:∵BD⊥AC于D,点E为AB的中点,
∴AB=2DE=2×5=10,
∴在Rt△ABD中,
BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8.
故答案为:8.
点评 此题主要考查了勾股定理以及直角三角形斜边的中线的性质,得出AB的长是解题关键.

练习册系列答案
相关题目
2.下列事件为必然事件的是( )
| A. | 如果a,b是实数,那么a•b=b•a | |
| B. | 抛掷一枚均匀的硬币,落地后正面朝上 | |
| C. | 汽车行驶到交通岗遇到绿色的信号灯 | |
| D. | 口袋中装有3个红球,从中随机摸出一球,这个球是白球 |
2.下列说法正确的是( )
| A. | 同位角相等 | |
| B. | 对顶角相等 | |
| C. | 两条直线被第三条直线所截,内错角相等 | |
| D. | 两条平行直线被第三条直线所截,同旁内角相等 |
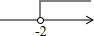
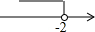
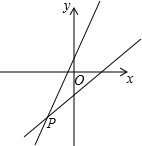 一次函数y=3x+b和y=ax-3的图象如图所示,其交点为P(-2,-5),则不等式3x+b>ax-3的解集在数轴上表示正确的是( )
一次函数y=3x+b和y=ax-3的图象如图所示,其交点为P(-2,-5),则不等式3x+b>ax-3的解集在数轴上表示正确的是( )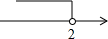

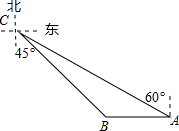 如图,码头A在码头B的正东方向,两个码头之间的距离为32海里,今有一货船由码头A出发,沿北偏西60°方向航行到达小岛C处,此时测得码头B在南偏东45°方向,求码头A与小岛C的距离.($\sqrt{3}$≈1.732,结果精确到0.01海里)
如图,码头A在码头B的正东方向,两个码头之间的距离为32海里,今有一货船由码头A出发,沿北偏西60°方向航行到达小岛C处,此时测得码头B在南偏东45°方向,求码头A与小岛C的距离.($\sqrt{3}$≈1.732,结果精确到0.01海里)