题目内容
17.给出四个数0,$\sqrt{5}$,$\frac{2}{7}$,-4,其中是无理数的是( )| A. | 0 | B. | $\sqrt{5}$ | C. | $\frac{2}{7}$ | D. | -4 |
分析 无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
解答 解:0,$\frac{2}{7}$,-4是有理数,
$\sqrt{5}$是无理数,
故选:B.
点评 此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.

练习册系列答案
相关题目
7.下列结论中,错误的是( )
| A. | 经过直线外一点,有且只有一条直线与这条直线平行 | |
| B. | 如果直线a,b,c满足:a∥b,c∥b,那么a∥c | |
| C. | 如果一个角的两边与另一个角的两边分别平行,那么这两个角相等 | |
| D. | 从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离 |
8.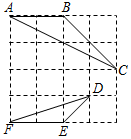 如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形顶点上,则tan∠ACB的值为( )
如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形顶点上,则tan∠ACB的值为( )
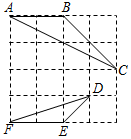 如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形顶点上,则tan∠ACB的值为( )
如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形顶点上,则tan∠ACB的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 3 |
6.从2开始,连续的偶数相加,它们的和的情况如下表:
(1)如果n=8时,那么S的值为72;
(2)根据表中的规律猜想:用n的代数式表示S的公式为S=2+4+6+8+…+2n=n(n+1);
(3)由上题的规律计算100+102+104+…+2014+2016的值(要有计算过程)
| 加数的个数n | 连续偶数的和S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
(2)根据表中的规律猜想:用n的代数式表示S的公式为S=2+4+6+8+…+2n=n(n+1);
(3)由上题的规律计算100+102+104+…+2014+2016的值(要有计算过程)
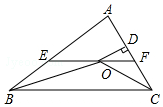 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
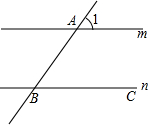 如图,直线m∥n,∠1=45°,C为直线n上的一动点,且在B点右边,若△ABC为等腰三角形,则∠BAC=67.5°或45°或90°.
如图,直线m∥n,∠1=45°,C为直线n上的一动点,且在B点右边,若△ABC为等腰三角形,则∠BAC=67.5°或45°或90°.