题目内容
12.圆内接四边形ABCD中,若∠A=2∠B=3∠C,则∠D的度数是112.5°.分析 先利用圆内接四边形对角互补得出∠A+∠C=∠B+∠D=180°,再把∠A=3∠C代入求出∠C=45°,那么∠A=135°=2∠B,再求出∠B=67.5°,则∠D=180°-∠B=112.5°.
解答 解:∵四边形ABCD是圆内接四边形,
∴∠A+∠C=∠B+∠D=180°,
∵∠A=2∠B=3∠C,
∴3∠C+∠C=180°,
∴∠C=45°,
∴∠A=135°=2∠B,
∴∠B=67.5°,
∴∠D=180°-∠B=112.5°.
故答案为:112.5°.
点评 此题主要考查了圆内接四边形的性质,掌握圆内接四边形对角互补是解题关键.

练习册系列答案
相关题目
2.下列说法:(1)图①可能是抛物线y=-x2+4x;(2)图②可能是抛物线y=(x-2)2-1;(3)图③可能是抛物线y=-3x2-4x+1;(4)图④可能是抛物线y=x2-6x+7.其中正确的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.一组数据6、4、a、3、2的平均数是5,则a的值为( )
| A. | 10 | B. | 5 | C. | 8 | D. | 12 |
17.给出四个数0,$\sqrt{5}$,$\frac{2}{7}$,-4,其中是无理数的是( )
| A. | 0 | B. | $\sqrt{5}$ | C. | $\frac{2}{7}$ | D. | -4 |
1. 实数x,y在数轴上的位置如图所示,则( )
实数x,y在数轴上的位置如图所示,则( )
 实数x,y在数轴上的位置如图所示,则( )
实数x,y在数轴上的位置如图所示,则( )| A. | 0<x<y | B. | x<y<0 | C. | x<0<y | D. | y<0<x |
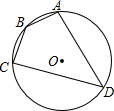 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠D=45°,则劣弧AC的长为π.
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠D=45°,则劣弧AC的长为π.