题目内容
已知:关于x的方程mx2+(3m+1)x+3=0.
(1)求证:不论m为任何实数,此方程总有实数根;
(2)如果该方程有两个不同的整数根,且m为正整数,求m的值;
(3)在(2)的条件下,令y=mx2+(3m+1)x+3,如果当x1=a与x2=a+n(n≠0)时有y1=y2,求代数式4a2+12an+5n2+16n+8的值.
(1)求证:不论m为任何实数,此方程总有实数根;
(2)如果该方程有两个不同的整数根,且m为正整数,求m的值;
(3)在(2)的条件下,令y=mx2+(3m+1)x+3,如果当x1=a与x2=a+n(n≠0)时有y1=y2,求代数式4a2+12an+5n2+16n+8的值.
考点:根的判别式,根与系数的关系
专题:计算题
分析:(1)分类讨论:当m=0时,原方程化为x+3=0,解得x=-3;当m≠0时,计算判别式得△=(3m-1)2,由于(3m-1)2≥0,则不论m为任何实数时总有两个实数根,所以不论m为任何实数时,方程 mx2+(3m+1)x+3=0总有实数根;
(2)先解方程mx2+(3m+1)x+3=0得到x1=-3,x2=-
,由于方程mx2+(3m+1)x+3=0有两个不同的整数根,且m为正整数,易得m=1;
(3)当m=1时得到y=x2+4x+3,当x1=a时,y1=a2+4a+3,当x2=a+n时,y2=(a+n)2+4(a+n)+3,则a2+4a+3=(a+n)2+4(a+n)+3,变形得 n(2a+n+4)=0,由于n≠0,所以2a=-n-4,然后变形4a2+12an+5n2+16n+8得到(2a)2+2a•6n+5n2+16n+8,再利用整体代入的方法计算.
(2)先解方程mx2+(3m+1)x+3=0得到x1=-3,x2=-
| 1 |
| m |
(3)当m=1时得到y=x2+4x+3,当x1=a时,y1=a2+4a+3,当x2=a+n时,y2=(a+n)2+4(a+n)+3,则a2+4a+3=(a+n)2+4(a+n)+3,变形得 n(2a+n+4)=0,由于n≠0,所以2a=-n-4,然后变形4a2+12an+5n2+16n+8得到(2a)2+2a•6n+5n2+16n+8,再利用整体代入的方法计算.
解答:(1)证明:当m=0时,原方程化为x+3=0,此时方程有实数根 x=-3;
当m≠0时,
∵△=(3m+1)2-12m=9m2-6m+1=(3m-1)2.
∵(3m-1)2≥0,
∴不论m为任何实数时总有两个实数根,
综上所述,不论m为任何实数时,方程 mx2+(3m+1)x+3=0总有实数根;
(2)解:当m≠0时,解方程mx2+(3m+1)x+3=0得 x1=-3,x2=-
,
∵方程mx2+(3m+1)x+3=0有两个不同的整数根,且m为正整数,
∴m=1;
(3)解:∵m=1,y=mx2+(3m+1)x+3,
∴y=x2+4x+3,
又∵当x1=a与x2=a+n(n≠0)时有y1=y2,
∴当x1=a时,y1=a2+4a+3,
当x2=a+n时,y2=(a+n)2+4(a+n)+3,
∴a2+4a+3=(a+n)2+4(a+n)+3,
化简得 2an+n2+4n=0,
即 n(2a+n+4)=0,
又∵n≠0,
∴2a=-n-4,
∴4a2+12an+5n2+16n+8
=(2a)2+2a•6n+5n2+16n+8
=(n+4)2+6n(-n-4)+5n2+16n+8
=24.
当m≠0时,
∵△=(3m+1)2-12m=9m2-6m+1=(3m-1)2.
∵(3m-1)2≥0,
∴不论m为任何实数时总有两个实数根,
综上所述,不论m为任何实数时,方程 mx2+(3m+1)x+3=0总有实数根;
(2)解:当m≠0时,解方程mx2+(3m+1)x+3=0得 x1=-3,x2=-
| 1 |
| m |
∵方程mx2+(3m+1)x+3=0有两个不同的整数根,且m为正整数,
∴m=1;
(3)解:∵m=1,y=mx2+(3m+1)x+3,
∴y=x2+4x+3,
又∵当x1=a与x2=a+n(n≠0)时有y1=y2,
∴当x1=a时,y1=a2+4a+3,
当x2=a+n时,y2=(a+n)2+4(a+n)+3,
∴a2+4a+3=(a+n)2+4(a+n)+3,
化简得 2an+n2+4n=0,
即 n(2a+n+4)=0,
又∵n≠0,
∴2a=-n-4,
∴4a2+12an+5n2+16n+8
=(2a)2+2a•6n+5n2+16n+8
=(n+4)2+6n(-n-4)+5n2+16n+8
=24.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程根与系数的关系.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
下列说法正确的是( )
| A、-5是(-5)2的算术平方根 |
| B、16的平方根是±4 |
| C、2是-4的算术平方根 |
| D、9的平方根是3 |
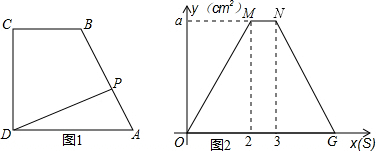
 如图,请画出△ABC关于点A的对称图形.
如图,请画出△ABC关于点A的对称图形.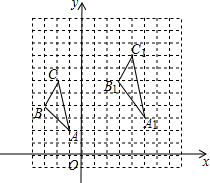 如图:
如图: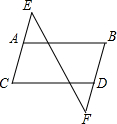 如图,现有以下3句话:①AB∥CD,②∠B=∠C.③∠E=∠F.请以其中2句话为条件,第三句话为结论构造命题.
如图,现有以下3句话:①AB∥CD,②∠B=∠C.③∠E=∠F.请以其中2句话为条件,第三句话为结论构造命题.