题目内容
14.已知抛物线y=-$\frac{1}{2}$x2+x+$\frac{3}{2}$.(1)写出抛物线的开口方向,对称轴和顶点坐标;
(2)求抛物线与x轴,y轴的交点坐标;
(3)指出x为何值时,y>0,y<0,y=0.
分析 (1)配方成顶点式,根据二次函数的性质是解题的关键;
(2)分别求出y=0时x的值和x=0时y的值可得答案;
(3)由抛物线的开口方向及其与x轴的交点可得答案.
解答 解:(1)∵y=-$\frac{1}{2}$x2+x+$\frac{3}{2}$=-$\frac{1}{2}$(x-1)2+2,
∴抛物线的开口向下,对称轴为直线x=1,顶点坐标为(1,2);
(2)当y=0时,有-$\frac{1}{2}$x2+x+$\frac{3}{2}$=0,
解得:x=-1或x=3,
∴抛物线与x轴的交点为(-1,0)和(3,0),
当x=0时,y=3,
∴抛物线与y轴的交点为(0,3);
(3)∵抛物线的开口向下,且抛物线与x轴的交点为(-1,0)和(3,0),
∴当-1<x<3时,y>0;
当x=-1或x=3时,y=0;
当x<-1或x>3时,y<0.
点评 本题主要考查二次函数的性质及抛物线与x轴的交点,熟练掌握二次函数的图象与性质是解题的关键.

练习册系列答案
相关题目
4.下列实数中,属于无理数的是( )
| A. | -3 | B. | 3.14 | C. | $\frac{22}{7}$ | D. | $\sqrt{8}$ |
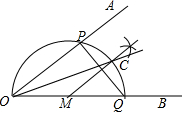 已知∠AOB,作图.
已知∠AOB,作图.
 已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从A出发,沿AC方向,以每秒1个单位的速度向终点C运动,设点P运动时间为t秒.
已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从A出发,沿AC方向,以每秒1个单位的速度向终点C运动,设点P运动时间为t秒.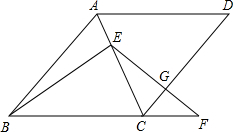 在菱形ABCD中,点E在对角线AC上,点F在BC的延长线上,EF=EB,EF与CD相交于点G.
在菱形ABCD中,点E在对角线AC上,点F在BC的延长线上,EF=EB,EF与CD相交于点G.