题目内容
2．
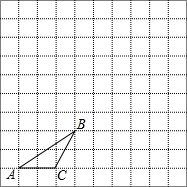如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）．（1）将△ABC绕点B顺时针旋转90°得到△A′BC′，请画出△A′BC′．
（2）求BA边旋转到BA′位置时所扫过图形的面积．
分析 （1）利用旋转的性质得出各对应点位置，再顺次连结即可求解；
（2）先根据勾股定理得到AB的长，再利用扇形面积公式得出答
解答 解：（1）如图所示：△A′BC′即为所求，
（2）∵AB=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$，
∴BA边旋转到BA″位置时所扫过图形的面积为：$\frac{90π×（\sqrt{13}）^{2}}{360}$=$\frac{13π}{4}$．
点评 此题主要考查了旋转变换、勾股定理以及扇形面积，得出对应点位置是解题关键．
练习册系列答案
相关题目
12．关于x的分式方程$\frac{m}{x-5}=\frac{x}{x-5}$，下列说法正确的是（ ）
| A． | 方程的解是x=m | B． | m＞0时，方程的解是正数 | ||
| C． | m＜0时，方程的解是正数 | D． | 无论m取何值，方程都不会无解 |
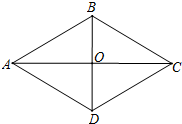如图，在菱形ABCD中，对角线AC与BD相交于点O，∠BAD=60°，BD=4，求菱形的边长AB和对角线AC的长．
将一根长为6m的木条做成如图形状的长方形框架，设AB=x（m），要求x不能小于0.5m．
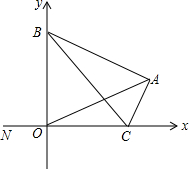如图所示，在平面直角坐标系xOy中，△ABC的顶点B是y轴正半轴上一个定点，D是BO的中点．点C在x轴上，A在第一象限，且满足AB=AO，N是x轴负半轴上一点，∠BCN=∠BAO=α．
如图，已知线段AB=4，延长线段AB到C，使BC=2AB，点D是AC的中点．求：