题目内容
10.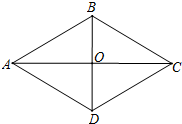 如图,在菱形ABCD中,对角线AC与BD相交于点O,∠BAD=60°,BD=4,求菱形的边长AB和对角线AC的长.
如图,在菱形ABCD中,对角线AC与BD相交于点O,∠BAD=60°,BD=4,求菱形的边长AB和对角线AC的长.
分析 根据菱形的性质结合等边三角形的判定与性质得出△ABD是等边三角形,可求出AD的长,再根据特殊角的锐角三角函数值进而求出AC的长.
解答 解:
∵在菱形ABCD中,对角线AC与BD相交于点O,∠BAD=60°,BD=4,
∴AD=AB,则△ABD是等边三角形,
∴AB=AD=CD=BC=4,∠DAC=30°,
故AO=4cos30°=2$\sqrt{3}$,
则AC=4$\sqrt{3}$.
点评 此题主要考查了菱形的性质以及等边三角形的判定与性质,求出OA的长是解题关键.

练习册系列答案
相关题目
5.关于矩形性质,下列说法不正确的是( )
| A. | 四个角都是直角 | |
| B. | 既是轴对称图形,也是中心对称图形 | |
| C. | 对角线互相垂直 | |
| D. | 对角线互相平分且相等 |
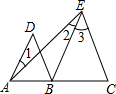 根据下列证明过程填空:
根据下列证明过程填空: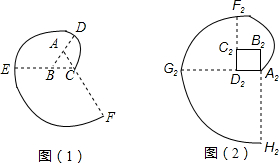
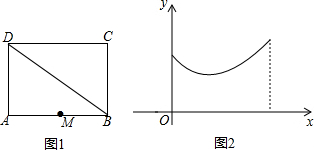 如图1,正方形ABCD中,点M是AB的中点,点P在某条线段上匀速运动,若运动的时间为x,点P与点M之间的距离为y,且表示y与x的函数关系的图象大致如图2所示,则点P的运动路线可能是( )
如图1,正方形ABCD中,点M是AB的中点,点P在某条线段上匀速运动,若运动的时间为x,点P与点M之间的距离为y,且表示y与x的函数关系的图象大致如图2所示,则点P的运动路线可能是( )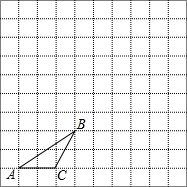 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).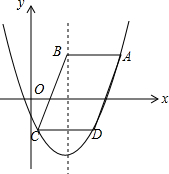 如图,在平面直角坐标系中,?ABCD的顶点A、C、D均在抛物线y=a(x-2)2+k(a>0)上,点B在抛物线的对称轴上,且AB∥x轴,若点A的横坐标为m,则点D的横坐标为$\frac{m+2}{2}$(用含m的代数式表示).
如图,在平面直角坐标系中,?ABCD的顶点A、C、D均在抛物线y=a(x-2)2+k(a>0)上,点B在抛物线的对称轴上,且AB∥x轴,若点A的横坐标为m,则点D的横坐标为$\frac{m+2}{2}$(用含m的代数式表示).