题目内容
若关于x的方程（m+1）x2+x+m2-2m-3=0有一个根为0，则m的值是（ ）
| A、-1 | B、3 |
| C、-1或3 | D、1或-3 |
考点：一元二次方程的解
专题：
分析：根据关于x的方程x2+mx-2m2=0的一个根为1，可将x=1代入方程，即可得到关于m的方程，解方程即可求出m值．
解答：解：把x=0代入方程可得m2-2m-3=0，
∴m2-2m-3=0，
解得：m=3或-1．
∵m+1≠0，
∴m≠-1
故选：B．
∴m2-2m-3=0，
解得：m=3或-1．
∵m+1≠0，
∴m≠-1
故选：B．
点评：此题主要考查了方程的解的意义和一元二次方程的解法．熟练运用公式法求得一元二次方程的解是解决问题的关键．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
如图，矩形ABCD中，AB=8，AD=3．点E从D向C以每秒1个单位的速度运动，以AE为一边在AE的右下方作正方形AEFG，同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动，当经过
如图，已知∠1=∠3，CD∥EF，试说明∠1=∠4．
如图，将周长为24的△ABC沿BC方向平移2个单位得到△DEF，则四边形ABFD的周长（ ）| A、26 | B、28 | C、30 | D、48 |
下列说法正确的是（ ）
| A、同位角相等 |
| B、对顶角相等 |
| C、同旁内角互补 |
| D、互补的角是邻补角 |
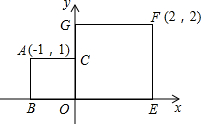如图，点A坐标为（-1，1），点F坐标为（2，2），正方形ABOC沿x轴向右平移，若与正方形OEFG重叠部分面积为| 1 |
| 2 |
A、（-
| ||||
B、（
| ||||
C、（-
| ||||
D、（
|
已知x、y是实数，
+y2-6y+9=0，则3x+y的值是（ ）
| 3x+4 |
A、
| ||
| B、7 | ||
| C、-1 | ||
D、-
|
