题目内容
 如图,将周长为24的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长( )
如图,将周长为24的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长( )| A、26 | B、28 | C、30 | D、48 |
考点:平移的性质
专题:
分析:根据平移的性质可得AD=CF=2,AC=DF,然后根据四边形的周长的定义列式计算即可得解.
解答:解:∵△ABC沿BC方向平移2个单位得到△DEF,
∴AD=CF=2,AC=DF,
∴四边形ABFD的周长=AB+(BC+CF)+DF+AD=AB+BC+AC+AD+CF,
∵△ABC的周长=24,
∴AB+BC+AC=24,
∴四边形ABFD的周长=24+2+2=28.
故选B.
∴AD=CF=2,AC=DF,
∴四边形ABFD的周长=AB+(BC+CF)+DF+AD=AB+BC+AC+AD+CF,
∵△ABC的周长=24,
∴AB+BC+AC=24,
∴四边形ABFD的周长=24+2+2=28.
故选B.
点评:本题考查了平移的性质,熟记性质得到相等的线段是解题的关键.

练习册系列答案
相关题目
 已知如图,DE是△ABC的中位线,AF是BC边上的中线,DE、AF交于点O.现有以下结论:
已知如图,DE是△ABC的中位线,AF是BC边上的中线,DE、AF交于点O.现有以下结论:①DE∥BC;②OD=
| 1 |
| 4 |
| 1 |
| 4 |
其中正确结论的个数为( )
| A、1 | B、2 | C、3 | D、4 |
若关于x的方程(m+1)x2+x+m2-2m-3=0有一个根为0,则m的值是( )
| A、-1 | B、3 |
| C、-1或3 | D、1或-3 |
∠1的对顶角是∠2,∠2的邻补角是∠3,若∠3=75°,则∠1的度数是( )
| A、75° | B、105° |
| C、90° | D、75°或105° |
计算结果为a14的式子是( )
| A、a7•a2 |
| B、a7+a7 |
| C、(a7)2 |
| D、(a7)7 |
 如图,BO、CO分别平分∠ABC和∠ACB,∠A=70°,则∠BOC=
如图,BO、CO分别平分∠ABC和∠ACB,∠A=70°,则∠BOC=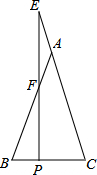 如图,在△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F,若AF=2,BF=3,则CE的长度为
如图,在△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F,若AF=2,BF=3,则CE的长度为