题目内容
 如图,已知∠1=∠3,CD∥EF,试说明∠1=∠4.
如图,已知∠1=∠3,CD∥EF,试说明∠1=∠4.解:∵∠1=∠3
又∠2=∠3
∴∠1=
∴
又∵CD∥EF
∴AB∥
∴∠1=∠4
考点:平行线的判定与性质
专题:推理填空题
分析:求出∠1=∠2,根据平行线的判定推出AB∥CD∥EF,根据平行线的性质得出即可.
解答:解:∵∠1=∠3(已知),
∵∠2=∠3(对顶角相等),
∴∠1=∠2(等量代换),
∴AB∥CD,
∵CD∥EF(已知),
∴AB∥EF,
∴∠1=∠4(两直线平行,同位角相等),
故答案为:(已知),(对顶角相等),∠2,AB,CD,(已知),EF,(两直线平行,同位角相等).
∵∠2=∠3(对顶角相等),
∴∠1=∠2(等量代换),
∴AB∥CD,
∵CD∥EF(已知),
∴AB∥EF,
∴∠1=∠4(两直线平行,同位角相等),
故答案为:(已知),(对顶角相等),∠2,AB,CD,(已知),EF,(两直线平行,同位角相等).
点评:本题考查了平行线的性质和判定的应用,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
若不等式组
的解集是x<2,则a的取值范围是( )
|
| A、a<2 | B、a≤2 |
| C、a>2 | D、a≥2 |
若关于x的方程(m+1)x2+x+m2-2m-3=0有一个根为0,则m的值是( )
| A、-1 | B、3 |
| C、-1或3 | D、1或-3 |
下列各式中正确的是( )
A、
| ||
B、±
| ||
C、
| ||
D、
|
 如图,直线AB、CD相交于点O,已知∠AOC+∠BOD=90°,则∠BOC=( )
如图,直线AB、CD相交于点O,已知∠AOC+∠BOD=90°,则∠BOC=( )| A、90° | B、145° |
| C、125° | D、135° |
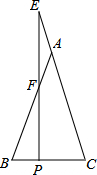 如图,在△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F,若AF=2,BF=3,则CE的长度为
如图,在△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F,若AF=2,BF=3,则CE的长度为