题目内容
在平面直角坐标系中,点P(k-1,k+1)在x轴上,则点P坐标为 .
考点:点的坐标
专题:
分析:根据x轴上点的纵坐标为0列出方程求解即可.
解答:解:∵点P(k-1,k+1)在x轴上,
∴k+1=0,
解得k=-1,
∴k-1=-1-1=-2,
∴点P的坐标为(-2,0).
故答案为:(-2,0).
∴k+1=0,
解得k=-1,
∴k-1=-1-1=-2,
∴点P的坐标为(-2,0).
故答案为:(-2,0).
点评:本题考查了点的坐标,熟记x轴上点的纵坐标为0是解题的关键.

练习册系列答案
相关题目
若关于x的方程(m+1)x2+x+m2-2m-3=0有一个根为0,则m的值是( )
| A、-1 | B、3 |
| C、-1或3 | D、1或-3 |
下列算式不能用平方差公式计算的是( )
| A、(3a+b)(-b-3a) |
| B、(a+b)(a-b) |
| C、(2x+y)(-2x+y) |
| D、(-m+n)(-m-n) |
 如图,BO、CO分别平分∠ABC和∠ACB,∠A=70°,则∠BOC=
如图,BO、CO分别平分∠ABC和∠ACB,∠A=70°,则∠BOC=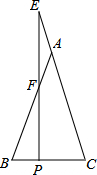 如图,在△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F,若AF=2,BF=3,则CE的长度为
如图,在△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F,若AF=2,BF=3,则CE的长度为