题目内容
9.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
| A. | ac<0 | B. | 当x>1时,y的值随x的增大而减小 | ||
| C. | 3是方程ax2+(b-1)x+c=0的一个根 | D. | 当-1<x<3时,ax2+(b-1)x+c>0 |
分析 利用表中各对应点的特征和抛物线的对称性得到c=3,抛物线的对称轴为直线x=$\frac{3}{2}$,顶点坐标为(1,5),所以抛物线开口向上,则可对A进行判断;根据二次函数的性质可对B进行判断;利用抛物线过点(-1,-1),(3,3)得到抛物线与直线y=x相交于点(-1,-1),(3,3),则可对C进行判断;利用函数图象可得当-1<x<3时,ax2+bx+c>x,则可对D进行判断.
解答 解:∵抛物线经过点(0,3)和(3,3),
∴c=3,抛物线的对称轴为直线x=$\frac{3}{2}$,顶点坐标为(1,5),
∴抛物线开口向上,
∴a<0,
∴ac<0,所以A选项的结论正确;
当x>$\frac{3}{2}$时,y的值随x的增大而减小,所以B选项的结论错误;
∵抛物线过点(-1,-1),(3,3),
即抛物线与直线y=x相交于点(-1,-1),(3,3),
∴3和-1是方程ax2+bx+c=x的根,所以C选项的结论正确;
当-1<x<3时,ax2+bx+c>x,
即ax2+(b-1)x+c>0,所以D选项的结论正确.
故选B.
点评 本题考查了二次函数与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c).也考查了二次函数的性质.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
4.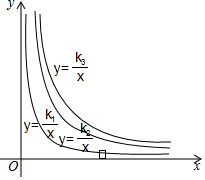 甲、乙、丙三人直立在相同大小的平板上,平板对水平地面的压强y(帕)与平板面积x(m)的关系分别如图中的y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$,则当平板面积增加量相同时,甲、乙、丙三人所站的平板对水平地面的压强变化的关系是( )
甲、乙、丙三人直立在相同大小的平板上,平板对水平地面的压强y(帕)与平板面积x(m)的关系分别如图中的y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$,则当平板面积增加量相同时,甲、乙、丙三人所站的平板对水平地面的压强变化的关系是( )
 甲、乙、丙三人直立在相同大小的平板上,平板对水平地面的压强y(帕)与平板面积x(m)的关系分别如图中的y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$,则当平板面积增加量相同时,甲、乙、丙三人所站的平板对水平地面的压强变化的关系是( )
甲、乙、丙三人直立在相同大小的平板上,平板对水平地面的压强y(帕)与平板面积x(m)的关系分别如图中的y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$,则当平板面积增加量相同时,甲、乙、丙三人所站的平板对水平地面的压强变化的关系是( )| A. | 甲的压强增加量>乙压强增加量>乙压强增加量 | |
| B. | 甲的压强减少量>乙压强减少量>乙压强减少量 | |
| C. | 乙的压强减少量>甲压强减少量>丙的压强减少量 | |
| D. | 丙的压强减少量>乙压强减少量>甲压强减少量 |
14.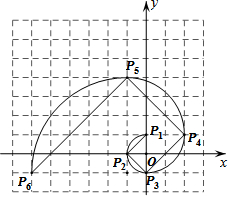 我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧$\widehat{{P_1}{P_2}}$,$\widehat{{P_2}{P_3}}$,$\widehat{{P_3}{P_4}}$,…得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,…得到螺旋折线(如图),已知点P1(0,1),P2(-1,0),P3(0,-1),则该折线上的点P9的坐标为( )
我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧$\widehat{{P_1}{P_2}}$,$\widehat{{P_2}{P_3}}$,$\widehat{{P_3}{P_4}}$,…得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,…得到螺旋折线(如图),已知点P1(0,1),P2(-1,0),P3(0,-1),则该折线上的点P9的坐标为( )
 我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧$\widehat{{P_1}{P_2}}$,$\widehat{{P_2}{P_3}}$,$\widehat{{P_3}{P_4}}$,…得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,…得到螺旋折线(如图),已知点P1(0,1),P2(-1,0),P3(0,-1),则该折线上的点P9的坐标为( )
我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧$\widehat{{P_1}{P_2}}$,$\widehat{{P_2}{P_3}}$,$\widehat{{P_3}{P_4}}$,…得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,…得到螺旋折线(如图),已知点P1(0,1),P2(-1,0),P3(0,-1),则该折线上的点P9的坐标为( )| A. | (-6,24) | B. | (-6,25) | C. | (-5,24) | D. | (-5,25) |
18.下列命题中,正确的是( )
| A. | 对角线相等的平行四边形是菱形 | |
| B. | 有两边及一角相等的两个三角形全等 | |
| C. | 同位角相等 | |
| D. | 直角三角形斜边上的中线等于斜边的一半 |
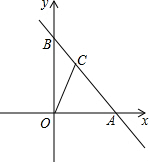 如图,直线y=-x+4与x轴交于点A,与y轴交于点B,点C在AB上,AC=2BC.求点C的坐标.
如图,直线y=-x+4与x轴交于点A,与y轴交于点B,点C在AB上,AC=2BC.求点C的坐标. 已知矩形ABCD的长AB=2,AB边与x轴重合,双曲线y=$\frac{k}{x}$在第一象限内经过D点以及BC的中点E.
已知矩形ABCD的长AB=2,AB边与x轴重合,双曲线y=$\frac{k}{x}$在第一象限内经过D点以及BC的中点E.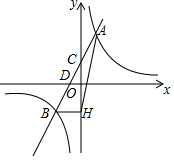 一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.
一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH. 如图,把正方形铁片OABC置于平面直角坐标系中,顶点A的坐标为(3,0),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置…,则正方形铁片连续旋转2017次后,点P的坐标为(6053,2).
如图,把正方形铁片OABC置于平面直角坐标系中,顶点A的坐标为(3,0),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置…,则正方形铁片连续旋转2017次后,点P的坐标为(6053,2).