题目内容
5.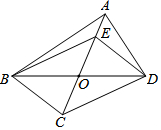 如图,在四边形ABCD中,对角线AC,BD相交于点O,且OB=OD.点E在线段OA上,连结BE,DE.给出下列条件:①OC=OE;②AB=AD;③BC⊥CD;④∠CBD=∠EBD.请你从中选择两个条件,使四边形BCDE是菱形,并给予证明.你选择的条件是:①②或①④或②④(只填写序号).
如图,在四边形ABCD中,对角线AC,BD相交于点O,且OB=OD.点E在线段OA上,连结BE,DE.给出下列条件:①OC=OE;②AB=AD;③BC⊥CD;④∠CBD=∠EBD.请你从中选择两个条件,使四边形BCDE是菱形,并给予证明.你选择的条件是:①②或①④或②④(只填写序号).
分析 可以选①②或①④或②④,根据菱形的判定方法一一判断即可.
解答 解:方法一:选①②.
∵OB=OD,OC=OE,
∴四边形BCDE是平行四边形,
∵AB=AD,OB=OD,
∴AO⊥BD,即EC⊥BD,
∴平行四边形BCDE是菱形.,
方法二:选①④.
∵OB=OD,OC=OE,
∴四边形BCDE是平行四边形,
∴BC∥DE,
∴∠CBD=∠BDE,
∵∠CBD=∠EBD,
∴∠BDE=∠EBD,
∴BE=DE,
∴平行四边形BCDE是菱形.
方法三:选②④.
解法一:∵AB=AD,OB=OD,
∴AO⊥BD,即EC⊥BD,
∴∠BOC=∠BOE=90°,
∵∠CBD=∠EBD,BO=BO,
∴△BOC≌△BOE,
∴OE=OC,
又∵OB=OD,
∴四边形BCDE是平行四边形,
又∵EC⊥BD,
∴平行四边形BCDE是菱形.
解法二:∵AB=AD,OB=OD,
∴AO⊥BD,即EC⊥BD,
∴EC垂直平分BD,
∴BE=DE,BC=DC,
∵∠BOC=∠BOE=90°,∠CBD=∠EBD,BO=BO,
∴△BOC≌△BOE,
∴BE=BC,
∴BE=DE=BC=DC,
∴四边形BCDE是菱形.
点评 本题考查全等三角形的判定和性质、平行四边形的判定和性质、菱形的判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
17.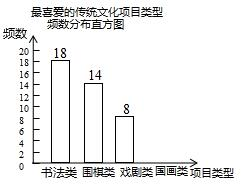 某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表
根据以上信息完成下列问题:
(1)频数分布表中a=0.36,b=10;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
 某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.最喜爱的传统文化项目类型频数分布表
| 项目类型 | 频数 | 频率 |
| 书法类 | 18 | a |
| 围棋类 | 14 | 0.28 |
| 喜剧类 | 8 | 0.16 |
| 国画类 | b | 0.20 |
(1)频数分布表中a=0.36,b=10;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
15.某班10名学生校服尺寸与对应人数如下表所示:
则这10名学生校服尺寸的中位数为170cm.
| 尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
| 学生人数(人) | 1 | 3 | 2 | 2 | 2 |
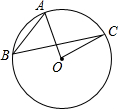 如图,OA、OC是⊙O的半径,点B在⊙O上,连接AB、BC,若∠ABC=40°,则∠AOC=80度.
如图,OA、OC是⊙O的半径,点B在⊙O上,连接AB、BC,若∠ABC=40°,则∠AOC=80度.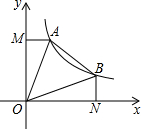 如图,一次函数y=-x+b(b>0)的图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A、B两点,连接OA、OB,AM⊥y轴,BN⊥x轴,垂足分别为M、N.下列结论:
如图,一次函数y=-x+b(b>0)的图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A、B两点,连接OA、OB,AM⊥y轴,BN⊥x轴,垂足分别为M、N.下列结论: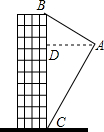 如图,航拍无人机从点A处测得一幢建筑物顶部B的仰角为32°,测得底部C的仰角为62°,此时航拍无人机与该建筑物的水平距离AD为54米,求该建筑物的高度BC(精确到0.1米,参考数据:sin 32°=0.530,cos32°=0.848,tan32°=0.625,sin 62°=0.883,cos62°=0.469,tan62°=1.88)
如图,航拍无人机从点A处测得一幢建筑物顶部B的仰角为32°,测得底部C的仰角为62°,此时航拍无人机与该建筑物的水平距离AD为54米,求该建筑物的高度BC(精确到0.1米,参考数据:sin 32°=0.530,cos32°=0.848,tan32°=0.625,sin 62°=0.883,cos62°=0.469,tan62°=1.88)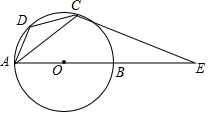 如图,AB为⊙O的直径,AD为弦,过⊙O上一点C作⊙O的切线交AB的延长线于E,且∠DCA=∠E.
如图,AB为⊙O的直径,AD为弦,过⊙O上一点C作⊙O的切线交AB的延长线于E,且∠DCA=∠E.