题目内容
18.计算:(1)$\sqrt{12}-2\sqrt{20}+5\sqrt{\frac{4}{5}}$
(2)$\sqrt{24}$+4$\sqrt{\frac{3}{8}}$-$\sqrt{3}$×$\sqrt{18}$+$\frac{\sqrt{84}}{\sqrt{14}}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先根据二次根式的乘除法则运算,然后化简后合并即可.
解答 解:(1)原式=2$\sqrt{3}$-4$\sqrt{5}$+2$\sqrt{5}$
=2$\sqrt{3}$-2$\sqrt{5}$;
(2)原式=2$\sqrt{6}$+$\sqrt{6}$-$\sqrt{3×18}$+$\sqrt{\frac{84}{14}}$
=2$\sqrt{6}$+$\sqrt{6}$-3$\sqrt{6}$+$\sqrt{6}$
=$\sqrt{6}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
3.某中学为筹备校庆,准备印制一批纪念册,每册由4张彩页,6张黑白页构成.印制该纪念册的总费用由制版费和印刷费两部分组成,其中制版费的价格为:彩页300元/张,黑白页50元/张;印刷费用与印数的关系见表:
(1)印制这批纪念册需制版费1500元,印制1千册纪念册的印刷费13000元;
(2)若印制这批纪念册共需y元,则:
①当1≤x<5时,求y关于x的函数表达式;
②当y≤60 080元,最多能印多少册?
| 印数x(千册) | 1≤x<5 | x≥5 |
| 彩色(元/张) | 2.2 | 2.0 |
| 黑白(元/张) | 0.7 | 0.6 |
(2)若印制这批纪念册共需y元,则:
①当1≤x<5时,求y关于x的函数表达式;
②当y≤60 080元,最多能印多少册?
3.已知点A(-1,y1),B(2,y2),C(3,y3)都在反比例函数y=-$\frac{5}{x}$的图象上,则下列结论中正确的是( )
| A. | y1<y2<y3 | B. | y2<y3<y1 | C. | y3<y2<y1 | D. | y1<y3<y2 |
8.某家具厂销售1套A种款式和2套B种款式的家具的利润为1400元,销售2套A种款式和3套B种款式家具的利润为2400元
(1)求每套A种款式和每套B种款式家具的销售利润;
(2)该家具厂计划用甲种板材200m2,乙种板材250m2生产A、B两种款式的家具,每套所需板材情况如表:
设甲种板材全部用完时恰好生产A款家具x套,两种款式家具全部售完时的销售利润为y元.
①求y与x之间的函数关系式;
②用这些板材生产的A、B两款家具,最大销售利润是多少?
(1)求每套A种款式和每套B种款式家具的销售利润;
(2)该家具厂计划用甲种板材200m2,乙种板材250m2生产A、B两种款式的家具,每套所需板材情况如表:
| 甲种板材(m2) | 乙种板材(m2) | |
| A款 | 3 | 6 |
| B款 | 5 | 4 |
①求y与x之间的函数关系式;
②用这些板材生产的A、B两款家具,最大销售利润是多少?
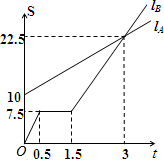 如图,LA,LB分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系.根据图象,回答下列问题:
如图,LA,LB分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系.根据图象,回答下列问题: 如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=2,则两平行线AD与BC间的距离为( )
如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=2,则两平行线AD与BC间的距离为( )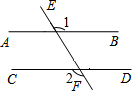 如图,直线AB,CD被EF所截,且AB∥CD,若∠1=126°,则∠2=126°.
如图,直线AB,CD被EF所截,且AB∥CD,若∠1=126°,则∠2=126°.