题目内容
9.观察下列等式:第1个等式:a1=$\frac{1}{1+\sqrt{2}}$=$\sqrt{2}$-1; 第2个等式:a2=$\frac{1}{\sqrt{2}+\sqrt{3}}$=$\sqrt{3}$-$\sqrt{2}$;
第3个等式:a3=$\frac{1}{\sqrt{3}+2}$=2-$\sqrt{3}$; 第4个等式:a4=$\frac{1}{2+\sqrt{5}}$=$\sqrt{5}$-2;
…
按上述规律,回答以下问题:
(1)请写出第n个等式:an=$\sqrt{n+1}$-$\sqrt{n}$;
(2)求a1+a2+a3+…+an的值.
分析 (1)原式仿照阅读材料中的方法:结果与分母只差一个符号,根据此规律求出值即可;
(2)分别将阅读材料中结果依次代入,互为相反数为0,化简即可.
解答 解:(1)an=$\frac{1}{\sqrt{n}+\sqrt{n+1}}$=$\sqrt{n+1}$-$\sqrt{n}$,
故答案为:$\sqrt{n+1}$-$\sqrt{n}$;
(2)a1+a2+a3+…+an,
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+…+$\sqrt{n+1}$-$\sqrt{n}$,
=-1+$\sqrt{n+1}$.
点评 此题考查了分母有理化,弄清阅读材料中的方法是解本题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
17.下列计算结果错误的是( )
| A. | (ab)7÷(ab)3=(ab)4 | B. | (x2 )3÷(x3 )2=x | ||
| C. | (-$\frac{2}{3}$m)4÷(-$\frac{2}{3}$m)2=(-$\frac{2}{3}$m)2 | D. | (5a)6÷(-5a)4=25a2 |
4.在平面直角坐标系中,线段A′B′是由线段AB经过平移得到的,已知点A(-2,1)的对应点为A′(3,-1),点B的对应点为B′(4,0),则点B的坐标为( )
| A. | (9,-1) | B. | (-1,0) | C. | (3,-1) | D. | (-1,2) |
14. 如图,在?ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE,则下列结论:①CF=AE;②OE=OF;③DE=BF;④图中共有四对全等三角形.其中正确结论的个数是( )
如图,在?ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE,则下列结论:①CF=AE;②OE=OF;③DE=BF;④图中共有四对全等三角形.其中正确结论的个数是( )
 如图,在?ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE,则下列结论:①CF=AE;②OE=OF;③DE=BF;④图中共有四对全等三角形.其中正确结论的个数是( )
如图,在?ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE,则下列结论:①CF=AE;②OE=OF;③DE=BF;④图中共有四对全等三角形.其中正确结论的个数是( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
18. 如图,AB∥CD,下列结论中错误的是( )
如图,AB∥CD,下列结论中错误的是( )
 如图,AB∥CD,下列结论中错误的是( )
如图,AB∥CD,下列结论中错误的是( )| A. | ∠2+∠3=180° | B. | ∠2+∠5=180° | C. | ∠3+∠4=180° | D. | ∠1=∠2 |
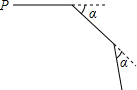 小明从P点出发,沿直线前进10米后向右转a,接着沿直线前进10米,再向右转a,…,照这样走下去,第一次回到出发地点P时,一共走了120米,则a的度数是30°.
小明从P点出发,沿直线前进10米后向右转a,接着沿直线前进10米,再向右转a,…,照这样走下去,第一次回到出发地点P时,一共走了120米,则a的度数是30°.