题目内容
20.已知x+y=4,xy=3,求下列代数式的值:(1)x2+y2;
(2)x2-y2.
分析 (1)把x+y=4两边平方,利用完全平方公式化简,再将xy=3代入计算即可求出值;
(2)利用完全平方公式及平方根定义求出x-y的值,原式利用平方差公式分解后,将各自的值代入计算即可求出值.
解答 解:(1)把x+y=4两边平方得:(x+y)2=x2+2xy+y2=16,
将xy=3代入得:x2+y2=10;
(2)∵(x-y)2=(x+y)2-4xy,x+y=4,xy=3,
∴(x-y)2=16-12=4,
∴x-y=2或x-y=-2,
则原式=(x+y)(x-y)=8或-8.
点评 此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
相关题目
10.在△ABC中,∠A=$\frac{1}{3}$∠B=$\frac{1}{5}$∠C,则△ABC是( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 无法确定 |
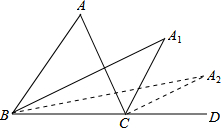 如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2016BC和∠A20l6CD的平分线交于点A2017,则∠A2017=$\frac{m}{{2}^{2017}}$°.
如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2016BC和∠A20l6CD的平分线交于点A2017,则∠A2017=$\frac{m}{{2}^{2017}}$°.