题目内容
14.如图,在小学我们通过观察、实验的方法得到了“三角形内角和是180°”的结论.小明通过这学期的学习知道:由观察、实验、归纳、类比、猜想得到的结论还需要通过证明来确认它的正确性.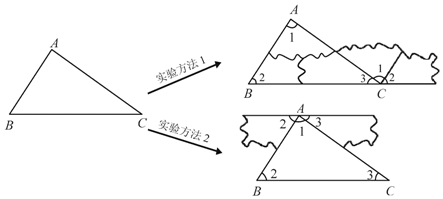
受到实验方法1的启发,小明形成了证明该结论的想法:实验1的拼接方法直观上看,是把∠1和∠2移动到∠3的右侧,且使这三个角的顶点重合,如果把这种拼接方法抽象为几何图形,那么利用平行线的性质就可以解决问题了.
小明的证明过程如下:
已知:如图,△ABC.求证:∠A+∠B+∠C=180°.
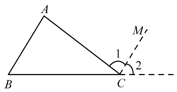
证明:延长BC,过点C作CM∥BA.
∴∠A=∠1(两直线平行,内错角相等),
∠B=∠2(两直线平行,同位角相等).
∵∠1+∠2+∠ACB=180°(平角定义),
∴∠A+∠B+∠ACB=180°.
请你参考小明解决问题的思路与方法,写出通过实验方法2证明该结论的过程.
分析 过点A作MN∥BC,利用平行线的性质得到∠MAB=∠B,∠NAC=∠C,进而利用平角的定义得到结论.
解答 已知:如图,△ABC.求证:∠A+∠B+∠C=180°.
证明:过点A作MN∥BC.
∴∠MAB=∠B,
∠NAC=∠C(两直线平行,内错角相等).
∵∠MAB+∠BAC+∠NAC=180°(平角定义),
∴∠B+∠BAC+∠C=180°.
点评 本题主要考查了三角形内角和定理以及平行线的性质,解题的关键是掌握两直线平行,内错角相等,此题难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.请思考下列命题的逆命题:①对顶角相等;②角平分线上的点到角两边的距离相等;③到线段两个端点距离相等的点在这条线段的垂直平分线上;④两个全等直角三角形的面积相等,其中逆命题不正确的命题的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9. 为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分:
为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分:
根据以上信息,解答下列问题:
(1)该调查方式是抽样调查;(填“普查”或者“抽样调查”)
(2)本次调查的家庭数为50户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是18%.
(3)若该小区共有1000户家庭,请估计该月用水量不超过9.0吨的家庭数.
 为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分:
为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分:| 分组 | 家庭用水量x/吨 | 家庭数/户 |
| A | 0≤x≤4.0 | 4 |
| B | 4.0<x≤6.5 | 13 |
| C | 6.5<x≤9.0 | |
| D | 9.0<x≤11.5 | |
| E | 11.5<x≤14.0 | 6 |
| F | x>14.0 | 3 |
(1)该调查方式是抽样调查;(填“普查”或者“抽样调查”)
(2)本次调查的家庭数为50户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是18%.
(3)若该小区共有1000户家庭,请估计该月用水量不超过9.0吨的家庭数.
6. 某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
表2:小王抽样调查单位10名职工的健康指数
表3:小李抽样调查单位10名职工的健康指数
根据上述材料回答问题:
(1)扇形统计图中老年职工所占部分的圆心角度数为72°
(2)小张、小王和小李三人中,小李的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
 某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.表1:小张抽样调查单位3名职工的健康指数
| 年龄 | 26 | 42 | 57 |
| 健康指数 | 97 | 79 | 72 |
| 年龄 | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
| 健康指数 | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | 60 |
| 年龄 | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
| 健康指数 | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
(1)扇形统计图中老年职工所占部分的圆心角度数为72°
(2)小张、小王和小李三人中,小李的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
3.在-$\frac{2}{3}$,0,-0.6,+2四个数中,最小的数是( )
| A. | $-\frac{2}{3}$ | B. | 0 | C. | -0.6 | D. | +2 |
4.下列调查,适合用全面调查方式的是( )
| A. | 了解一批灯泡的使用寿命是否合格 | |
| B. | 了解珠江河中鱼的各类 | |
| C. | 了解广东电视台珠江频道《今日关注》的收视率 | |
| D. | 了解某校七年级一班学生的视力状况 |
 如图,E为?ABCD的边AB延长线上的一点,且BE:AB=2:3,连接DE交BC于点F,则CF:AD=3:5.
如图,E为?ABCD的边AB延长线上的一点,且BE:AB=2:3,连接DE交BC于点F,则CF:AD=3:5.