题目内容
4. 如图,在△ABC中,AD⊥BC,垂足为D,E为AC上一点,BE交AD于F,且BF=AC,FD=CD,AD=3,求AB的长.
如图,在△ABC中,AD⊥BC,垂足为D,E为AC上一点,BE交AD于F,且BF=AC,FD=CD,AD=3,求AB的长.
分析 先证明Rt△BDF≌Rt△ADC,得AD=BD=3,由勾股定理求AB的长.
解答 解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△BDF和Rt△ADC中,
∵$\left\{\begin{array}{l}{BF=AC}\\{FD=CD}\end{array}\right.$,
∴Rt△BDF≌Rt△ADC(HL),
∴AD=BD=3,
在Rt△ABD中,AB2=AD2+BD2,
∴AB2=32+32,
AB=3$\sqrt{2}$.
点评 本题考查了直角三角形全等的性质和判定,直角三角形又是特殊的三角形,有它的特殊性,作为“HL”公理就是直角三角形独有的判定方法.所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件;同时本题还运用了勾股定理求线段的长.

练习册系列答案
相关题目
16. 如图,有两棵树,一棵树高8m,另一棵树高3m,两树相距12m.一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
如图,有两棵树,一棵树高8m,另一棵树高3m,两树相距12m.一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
 如图,有两棵树,一棵树高8m,另一棵树高3m,两树相距12m.一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
如图,有两棵树,一棵树高8m,另一棵树高3m,两树相距12m.一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )| A. | 12m | B. | 14m | C. | 13m | D. | 15m |
 如图,在梯形ABCD中,EF∥GH∥AD,已知EF和GH分梯形ABCD成三个彼此相似的梯形,BC=1,AD=8,求EF和HG的长.
如图,在梯形ABCD中,EF∥GH∥AD,已知EF和GH分梯形ABCD成三个彼此相似的梯形,BC=1,AD=8,求EF和HG的长.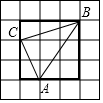 如图,在边长为1的格点图中,求△ABC的周长和面积.
如图,在边长为1的格点图中,求△ABC的周长和面积. 如图,已知∠AOB=60°,点P在OA上,OP=8,点M、N在边OB上,PM=PN,若MN=2,则OM=3.
如图,已知∠AOB=60°,点P在OA上,OP=8,点M、N在边OB上,PM=PN,若MN=2,则OM=3. 已知:如图,D、E、F是△ABC各边的中点,FG∥CD交ED的延长线于点G,AC=6.求GD的长度.
已知:如图,D、E、F是△ABC各边的中点,FG∥CD交ED的延长线于点G,AC=6.求GD的长度.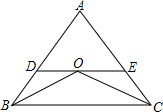 如图,已知OB、OC为△ABC的角平分线,DE∥BC,△ADE的周长为10,BC长为8,求△ABC的周长.
如图,已知OB、OC为△ABC的角平分线,DE∥BC,△ADE的周长为10,BC长为8,求△ABC的周长.