题目内容
18．
如图，已知∠AOB=30°，点P在边OA上，点M、N在边OB上，且PM=PN=10，MN=12，则OP=16．
分析 过P作PD⊥OB于点D，由PM=PN，利用等腰三角形三线合一的性质得到D为MN中点，根据MN=12求出MD的长，然后结合勾股定理可以求得PD的长度，最后由含30度角的直角三角形的性质来求OP的长度．
解答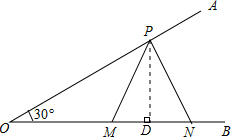 
解：过P作PD⊥OB于点D，
∵PM=PN=10，MN=12，
∴MD=$\frac{1}{2}$MN=6，
则在直角△OPD中，PD=$\sqrt{P{M}^{2}-D{N}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8．
又∵∠AOB=30°，
∴OP=2PD=16．
故答案是：16．
点评 此题考查了含30度直角三角形的性质，等腰三角形的性质，熟练掌握直角三角形的性质是解本题的关键．
练习册系列答案
相关题目
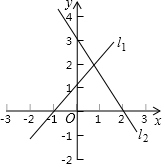已知：如图所示的坐标系中两直线l1、l2的交点坐标，可以看作哪个方程组的解？
如图，已知∠AOB=60°，点P在OA上，OP=8，点M、N在边OB上，PM=PN，若MN=2，则OM=3．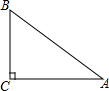
已知A，B，C三地位置如图所示，∠C=90°，A，C两地的距离是4km，B，C两地的距离是3km，则A，B两地的距离是5km．
已知：如图，D、E、F是△ABC各边的中点，FG∥CD交ED的延长线于点G，AC=6．求GD的长度．