题目内容
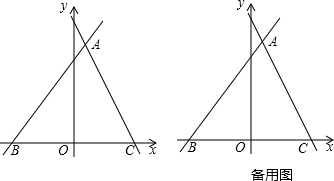
10. 如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,以下结论:
如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④∠BDC=$\frac{1}{2}$∠BAC.其中正确的结论有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据角平分线定义得出∠ABC=2∠ABD=2∠DBC,∠EAC=2∠EAD,∠ACF=2∠DCF,根据三角形的内角和定理得出∠BAC+∠ABC+∠ACB=180°,根据三角形外角性质得出∠ACF=∠ABC+∠BAC,∠EAC=∠ABC+∠ACB,根据已知结论逐步推理,即可判断各项.
解答 解:∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,∴①正确;
∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,∠ABC=∠ACB,
∴∠ABC=∠ACB=2∠DBC,
∴∠ACB=2∠ADB,∴②正确;
∵AD平分∠EAC,CD平分∠ACF,
∴∠DAC=$\frac{1}{2}$∠EAC,∠DCA=$\frac{1}{2}$∠ACF,
∵∠EAC=∠ACB+∠ACB,∠ACF=∠ABC+∠BAC,∠ABC+∠ACB+∠BAC=180°,
∴∠ADC=180°-(∠DAC+∠ACD)
=180°-$\frac{1}{2}$(∠EAC+∠ACF)
=180°-$\frac{1}{2}$(∠ABC+∠ACB+∠ABC+∠BAC)
=180°-$\frac{1}{2}$(180°-∠ABC)
=90°-$\frac{1}{2}$∠ABC,∴③正确;
∵∠ACF=2∠DCF,∠ACF=∠BAC+∠ABC,∠ABC=2∠DBC,∠DCF=∠DBC+∠BDC,
∴∠BAC=2∠BDC,∴④正确;
即正确的有4个,
故选A.
点评 本题考查了三角形外角性质,角平分线定义,平行线的判定,三角形内角和定理的应用,主要考察学生的推理能力,有一定的难度.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
20.二元一次方程组$\left\{\begin{array}{l}x+y=1\\ x-y=3\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
1.若a>b,则下列不等式变形正确的是( )
| A. | a+5<b+5 | B. | $\frac{a}{3}>\frac{b}{3}$ | C. | -4a>-4b | D. | 3a-2<3b-2 |
18.已知x1,x2是一元二次方程x2-4x+1=0的两个实数根,则x1x2-x1-x2的值等于( )
| A. | -3 | B. | 0 | C. | 3 | D. | 5 |
2.若a<b,则下列不等式中正确的是( )
| A. | 2a>2b | B. | a-b>0 | C. | -3a>-3b | D. | a-3<b-5 |
20.若Rt△ABC中,∠C=90°,且AB=10,BC=8,则AC的值是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |