题目内容
18.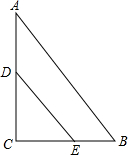 如图,在△ABC中,AB=10,AC=8,BC=6,DE∥AB,如图点D在AC上(与A、C不重合),点E在BC上.
如图,在△ABC中,AB=10,AC=8,BC=6,DE∥AB,如图点D在AC上(与A、C不重合),点E在BC上.(1)当△DEC的周长与四边形DABE的周长相等时,求DC的长.
(2)当△DEC的面积与四边形DABE的面积相等时,求DC的长.
分析 (1)由△CDE的周长与四边形DABE的周长相等,可得CD+CE=$\frac{1}{2}$×△ABC的周长,然后由相似三角形的对应边成比例,列出方程式求得答案.
(2)由DE∥AB,可得△DCE∽△ACB,根据相似三角形的面积比等于相似比的平方,即可求得答案;
解答  解:(1)∵△CDE的周长与四边形DABE的周长相等,
解:(1)∵△CDE的周长与四边形DABE的周长相等,
∴CD+DE+CE=AD+AB+BE+DE,
∴CD+CE=AD+AB+BE,
∴CD+CE=$\frac{1}{2}$×△ABC的周长,
∵在△ABC中,AB=10,AC=8,BC=6,
∴CD+CE=12,
∵DE∥AB,
∴△DCE∽△ACB,
∴$\frac{CD}{CA}$=$\frac{CE}{CB}$,
即$\frac{CD}{4}$=$\frac{12-CD}{6}$,
解得:CD=4.8;
(2)∵DE∥AB,
∴△DCE∽△ACB,
∴$\frac{{S}_{△DCE}}{{S}_{△ACB}}$=$(\frac{CD}{AC})^{2}$,
∵△CDE的面积与四边形DABE的面积相等,
∴$(\frac{CD}{AC})^{2}$=$\frac{1}{2}$,即$\frac{CD}{AC}$=$\frac{1}{\sqrt{2}}$,
∵AC=8,
∴CD=4$\sqrt{2}$.
点评 此题考查了相似三角形的判定与性质的运用.相似三角形的面积的比等于相似比的平方,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
7.⊙O的直径为10,圆心O到弦AB的距离为3,则弦AB的长是( )
| A. | 4 | B. | 6 | C. | 7 | D. | 8 |
 △ABC三个顶点A、B、C在平面直角坐标系中位置如图所示.将△ABC绕C点顺时针旋转90°,画出旋转后的△A1B1C,并写出A1、B1的坐标.
△ABC三个顶点A、B、C在平面直角坐标系中位置如图所示.将△ABC绕C点顺时针旋转90°,画出旋转后的△A1B1C,并写出A1、B1的坐标.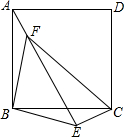 点E在正方形ABCD外,BE=4,CE=2,∠BEC=135°,将△BEC绕点B逆时针旋转得到△BFA,求FE、FC的长.
点E在正方形ABCD外,BE=4,CE=2,∠BEC=135°,将△BEC绕点B逆时针旋转得到△BFA,求FE、FC的长.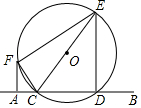 直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.
直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.