题目内容
8.已知-x=$\sqrt{2{x}^{2}+3xy-4{y}^{2}}$(y>0),求$\frac{x}{y}$的值.分析 将原式两边平方,分解因式后解方程得:x=-4y或x=y,得出$\frac{x}{y}$的值,再根据已知x、y的取值可知:x、y异号,商为负,得出结果.
解答 解:由题意得:x≤0,
-x=$\sqrt{2{x}^{2}+3xy-4{y}^{2}}$(y>0),
两边同时平方得:x2=2x2+3xy-4y2,
x2+3xy-4y2=0,
(x+4y)(x-y)=0,
x=-4y或x=y,
当x=-4y时,$\frac{x}{y}$=$\frac{-4y}{y}$=-4,
当x=y时,$\frac{x}{y}$=1,
∵x≤0,y>0
∴$\frac{x}{y}$≤0
∴$\frac{x}{y}$的值为-4.
点评 本题考查了分式和二次根据的性质与化简,注意:①分式的分母不为0,②二次根据的非负性,③将原式两边平方后扩大了值的范围,因此要考虑取值问题.

练习册系列答案
相关题目
19.已知10m=2,10n=3,则103m+2n=( )
| A. | 17 | B. | 72 | C. | 12 | D. | 36 |
16.某食品厂从生产的袋装食品中随机抽样检测20袋的质量是否符合标准质量,超过或不足的质量分别用正、负数表示,例如+3表示该袋食品超过标准质量3克,现记录如下:
(1)在抽取的样品中,任意挑选两袋,它们的质量相差最大多少克?
(2)食品包装袋中标有“净重500±2克”,这批样品中有几袋质量不合格?并请你计算出这20袋食品的合格率是多少?【产品的合格率=(一批产品中的合格产品数量÷这批产品总量)×100%】
(3)若标准质量为500克/袋,则这次抽样检测的总质量是多少克?
| 与标准质量的误差 (单位:克) | -4 | -2 | 0 | +1 | +2 | +3 |
| 袋数 | 5 | 3 | 3 | 4 | 2 | 3 |
(2)食品包装袋中标有“净重500±2克”,这批样品中有几袋质量不合格?并请你计算出这20袋食品的合格率是多少?【产品的合格率=(一批产品中的合格产品数量÷这批产品总量)×100%】
(3)若标准质量为500克/袋,则这次抽样检测的总质量是多少克?
17.在如图所示的某年12月份日历中,用长方形的方框圈出任意3×3个数.
(1)如果从左下角到右上角的“对角线”上的3个数字的和为54,那么这9个数的和为162,在这9个日期中,最后一天是26号;
(2)在这个月的日历中,用方框能否圈出“总和为171”的9个数?如果能,请求出这9个日期最后一天是几号;如果不能,请推测下个月的日历中,能否用方框圈出,如果能,请推测圈出的9个数中最后一天是星期几?
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
(2)在这个月的日历中,用方框能否圈出“总和为171”的9个数?如果能,请求出这9个日期最后一天是几号;如果不能,请推测下个月的日历中,能否用方框圈出,如果能,请推测圈出的9个数中最后一天是星期几?
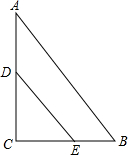 如图,在△ABC中,AB=10,AC=8,BC=6,DE∥AB,如图点D在AC上(与A、C不重合),点E在BC上.
如图,在△ABC中,AB=10,AC=8,BC=6,DE∥AB,如图点D在AC上(与A、C不重合),点E在BC上.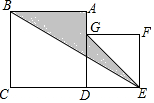 正方形ABCD与正方形DEFG如图所示摆放,正方形ABCD的边长为acm,正方形DEFG的边长为bcm.
正方形ABCD与正方形DEFG如图所示摆放,正方形ABCD的边长为acm,正方形DEFG的边长为bcm.