题目内容
6. 如图,菱形ABCD边长为2cm,∠ABC=60°,且M是BC边的中点,P是对角线BD上一动点,则PM+PC的最小值为$\sqrt{3}$.
如图,菱形ABCD边长为2cm,∠ABC=60°,且M是BC边的中点,P是对角线BD上一动点,则PM+PC的最小值为$\sqrt{3}$.
分析 根据菱形的性质,得知A、C关于BD对称,根据轴对称的性质,将PM+PC转化为AP+PM,再根据两点之间线段最短得知AM为PM+PC的最小值.
解答 解:∵四边形ABCD为菱形,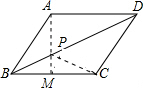
∴A、C关于BD对称,
∴连AM交BD于P,
则PM+PC=PM+AP=AM,
根据两点之间线段最短,AM的长即为PM+PC的最小值.
∵∠ABC=60°,
∴∠ABM=∠BAC=60°,
∴△ABC为等边三角形,
又∵BM=CM,
∴AM⊥BC,
∴AM=$\sqrt{A{B}^{2}-B{M}^{2}}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 此题考查了轴对称---最短路径问题,解答过程要利用菱形的性质及等腰三角形的性质,转化为两点之间线段最短的问题来解.

练习册系列答案
相关题目
17.若两条平行线被第三条直线所截,则一对同旁内角的角平分线( )
| A. | 互相平行 | B. | 互相垂直 | C. | 相交但不垂直 | D. | 互相垂直或平行 |
4.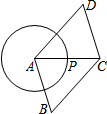 如图,点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=$\sqrt{3}$,则平行四边形ABCD面积的最大值为( )
如图,点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=$\sqrt{3}$,则平行四边形ABCD面积的最大值为( )
 如图,点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=$\sqrt{3}$,则平行四边形ABCD面积的最大值为( )
如图,点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=$\sqrt{3}$,则平行四边形ABCD面积的最大值为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 3 | D. | 3$\sqrt{3}$ |
5.用代入法解方程组$\left\{\begin{array}{l}2x+3y=7\\ 5x-y=9\end{array}\right.$先消去未知数( )最简便.
| A. | x | B. | y | ||
| C. | 两个中的任何一个都一样 | D. | 无法确定 |
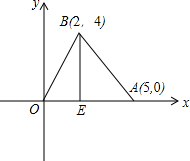 如图,在平面直角坐标系中,A(5,0),B(2,4),AB=5,BE垂直于x轴,垂足为点E,动点P从点A出发以3个单位/s的速度沿射线AB运动,动点Q从点O出发,在折线OA-AB上运动,在线段OA上以每秒5个单位速度运动,在AB上以每秒3个单位的速度,运动时间为t秒,若P、Q同时出发,点Q停止,点P随之停止运动.
如图,在平面直角坐标系中,A(5,0),B(2,4),AB=5,BE垂直于x轴,垂足为点E,动点P从点A出发以3个单位/s的速度沿射线AB运动,动点Q从点O出发,在折线OA-AB上运动,在线段OA上以每秒5个单位速度运动,在AB上以每秒3个单位的速度,运动时间为t秒,若P、Q同时出发,点Q停止,点P随之停止运动.