题目内容
11.(1)x4n+1÷x2n-1•x2n+1=x2n+3.(2)已知ax=2,ay=3,则ax-y=$\frac{2}{3}$.
(3)已知ax=2,ay=3,则a2x-y=$\frac{4}{3}$.
分析 (1)直接利用同底数幂的乘除运算法则求出答案;
(2)直接利用同底数幂的除法运算法则求出答案;
(2)结合幂的乘方运算法则以及利用同底数幂的除法运算法则求出答案.
解答 解:(1)x4n+1÷x2n-1•x2n+1=x4n+1-2n+1+2n+1=x2n+3.
故答案为:x2n+3.
(2)∵ax=2,ay=3,
∴ax-y=ax÷ay=$\frac{2}{3}$;
故答案为:$\frac{2}{3}$;
(3)∵ax=2,ay=3,
∴a2x-y=(ax)2÷ay=4÷3=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 此题主要考查了同底数幂的乘除运算法则,正确将原式变形是解题关键.

练习册系列答案
相关题目
9.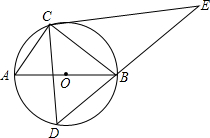 如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=10,AC=6,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=10,AC=6,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
 如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=10,AC=6,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=10,AC=6,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )| A. | $\frac{20}{3}$ | B. | $\frac{40}{3}$ | C. | 16 | D. | $\frac{64}{5}$ |
 如图,菱形ABCD边长为2cm,∠ABC=60°,且M是BC边的中点,P是对角线BD上一动点,则PM+PC的最小值为$\sqrt{3}$.
如图,菱形ABCD边长为2cm,∠ABC=60°,且M是BC边的中点,P是对角线BD上一动点,则PM+PC的最小值为$\sqrt{3}$.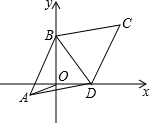 如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是5$\sqrt{3}$-5.
如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是5$\sqrt{3}$-5. 已知CA=CB,CD=CE,B、C、E在同一条直线上,∠BCA=∠DCE=60°.
已知CA=CB,CD=CE,B、C、E在同一条直线上,∠BCA=∠DCE=60°.