题目内容
14.已知,在正方形ABCD中,点F是AD上一点,且AF:FD=1:2,BF与AC交于点G,则△AFG与△BCG的面积之比是1:9.△BGC与△AGB的面积之比是3:1.分析 根据正方形的性质得AD=BC,AD∥BC,则利用AF:FD=1:2可得AF:BC=1:3,接着利用AF∥BC可判断△AGF∽△CGB,根据相似三角形的性质得$\frac{AG}{GC}$=$\frac{AF}{BC}$=$\frac{1}{3}$,$\frac{{S}_{△AFG}}{{S}_{△BCG}}$=($\frac{AF}{BC}$)2=$\frac{1}{9}$,然后利用三角形面积公式易得$\frac{{S}_{△BGC}}{{S}_{△AGB}}$=$\frac{CG}{AG}$=3.
解答 解:如图,
∵四边形ABCD为正方形,
∴AD=BC,AD∥BC,
∵AF:FD=1:2,
∴AF:BC=1:3,
∵AF∥BC,
∴△AGF∽△CGB,
∴$\frac{AG}{GC}$=$\frac{AF}{BC}$=$\frac{1}{3}$,$\frac{{S}_{△AFG}}{{S}_{△BCG}}$=($\frac{AF}{BC}$)2=($\frac{1}{3}$)2=$\frac{1}{9}$,
∴$\frac{{S}_{△BGC}}{{S}_{△AGB}}$=$\frac{CG}{AG}$=$\frac{3}{1}$=3.
故答案为1:9;3:1.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;相似三角形面积的比等于相似比的平分.也考查了正方形的性质.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
2.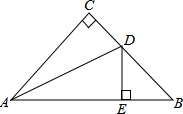 如图,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AB=6cm,则△DEB周长为( )
如图,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AB=6cm,则△DEB周长为( )
 如图,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AB=6cm,则△DEB周长为( )
如图,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AB=6cm,则△DEB周长为( )| A. | 4cm | B. | 6cm | C. | 10cm | D. | 14cm |
9.已知菱形的周长为16,有一个内角为60°,则菱形的面积为( )
| A. | $8\sqrt{3}$ | B. | $6\sqrt{3}$ | C. | $4\sqrt{3}$ | D. | $2\sqrt{3}$ |
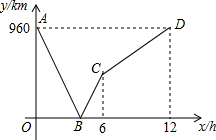 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据题中所给信息解答以下问题:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据题中所给信息解答以下问题: