题目内容
17.计算:(1)$\sqrt{18}$+$\sqrt{50}$-2$\sqrt{32}$+(-2)
(2)(6$\sqrt{\frac{x}{4}}$-2x$\sqrt{\frac{1}{x}}$)÷3$\sqrt{x}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的除法运算.
解答 解:(1)原式=3$\sqrt{2}$+5$\sqrt{2}$-8$\sqrt{2}$-2
=-2;
(2)原式=(3$\sqrt{x}$-2$\sqrt{x}$)÷3$\sqrt{x}$
=$\sqrt{x}$÷3$\sqrt{x}$
=$\frac{1}{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
8.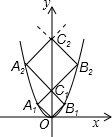 如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )
如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )
 如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )
如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )| A. | 2013 | B. | 2014 | C. | 2013$\sqrt{2}$ | D. | 2014$\sqrt{2}$ |
5.下列各数化简后为正数的是( )
| A. | +(-2) | B. | -(-2) | C. | -(+2) | D. | -|-2| |
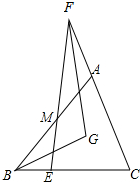 如图,已知FG是∠EFC的角平分线,BG是∠ABC的角平分线,
如图,已知FG是∠EFC的角平分线,BG是∠ABC的角平分线, 如图,?ABCD中,对角线AC、BD相交于点O,点E是CD的中点,则△DOE与△BCD的面积比为1:4.
如图,?ABCD中,对角线AC、BD相交于点O,点E是CD的中点,则△DOE与△BCD的面积比为1:4.