题目内容
16.已知扇形的圆心角为60°,半径为5,则扇形的周长为( )| A. | $\frac{5}{3}$π | B. | $\frac{5}{3}$π+10 | C. | $\frac{5}{6}$ | D. | $\frac{5}{6}$π+10 |
分析 先利用弧长公式计算出扇形的弧长,然后加上两个半径的长即可得到这个扇形的周长.
解答 解:扇形的弧长=$\frac{60•π•5}{180}$=$\frac{5}{3}$π,
所以扇形的周长=5+5+$\frac{5}{3}$π=10+$\frac{5}{3}$π.
故选B.
点评 本题考查了弧长的计算:记住弧长公式:l=$\frac{nπR}{180}$(弧长为l,圆心角度数为n,圆的半径为R),在弧长的计算公式中,n是表示1°的圆心角的倍数,n和180都不要带单位.

练习册系列答案
相关题目
11.已知点A(-4,y1),B(2,y2)都在直线y=-x+2上,则y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
8.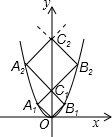 如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )
如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )
 如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )
如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )| A. | 2013 | B. | 2014 | C. | 2013$\sqrt{2}$ | D. | 2014$\sqrt{2}$ |
5.下列各数化简后为正数的是( )
| A. | +(-2) | B. | -(-2) | C. | -(+2) | D. | -|-2| |
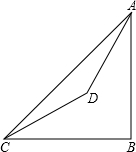 如图,在山脚C测得山顶A的仰角为45°,沿着倾斜角为30°的斜坡前进300米到达D出,D处测得山顶的仰角为60°,求山高AB(结果保留根号).
如图,在山脚C测得山顶A的仰角为45°,沿着倾斜角为30°的斜坡前进300米到达D出,D处测得山顶的仰角为60°,求山高AB(结果保留根号).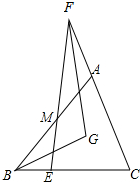 如图,已知FG是∠EFC的角平分线,BG是∠ABC的角平分线,
如图,已知FG是∠EFC的角平分线,BG是∠ABC的角平分线,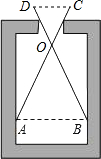 如图,用一个交叉卡钳(OA=OB,OC=OD)测量零件的内孔直径AB,若OC:OA=1:2,且量的CD=12mm,则零件的内孔直径AB是24mm.
如图,用一个交叉卡钳(OA=OB,OC=OD)测量零件的内孔直径AB,若OC:OA=1:2,且量的CD=12mm,则零件的内孔直径AB是24mm.