题目内容
20.已知x1,x2是方程x2-3x-3=0两根,则(x12-2x1-3)(x22-2x2-3)=-3.分析 先根据一元二次方程解的定义得到x12-3x1-3=0,x22-3x2-3=0,则x12=3x1+3,x22=3x2+3,原式原式可化简为x1•x1,然后利用根与系数的关系求解.
解答 解:∵x1,x2是方程x2-3x-3=0的两根,
∴x12-3x1-3=0,x22-3x2-3=0,
即x12=3x1+3,x22=3x2+3,
∴原式=(3x1+3-2x1-3)(3x2+3-2x2-3)
=x1•x1,
∵x1,x2是方程x2-3x-3=0的两根,
∴x1•x1=-3,
∴原式=-3.
故答案为:-3.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了一元二次方程解的定义.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
11.已知点A(-4,y1),B(2,y2)都在直线y=-x+2上,则y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
8.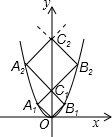 如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )
如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )
 如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )
如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )| A. | 2013 | B. | 2014 | C. | 2013$\sqrt{2}$ | D. | 2014$\sqrt{2}$ |
5.下列各数化简后为正数的是( )
| A. | +(-2) | B. | -(-2) | C. | -(+2) | D. | -|-2| |
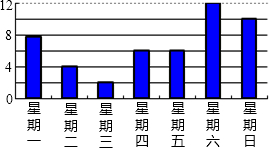 如图是明明作的一周的零用钱开支的统计图(单位:元)
如图是明明作的一周的零用钱开支的统计图(单位:元)